Sayıların Dili, OYUN, Temmuz 2007

2 Milenyumluk Gizemli Sayı : π

Timur Karaçay

tkaracay@baskent.edu.tr

Bu gizemli sayıyı yaratan basit bir sorudur:

Bir çemberin çevre uzunluğu çapının kaç katıdır?

Bu soru, insanoğlunu 2000 yıldan fazla uğraştırdı. Bütün zamanların en akıllı insanları, adına pi denen bu katsayıyı bulmak için uğraş verdi. Belki, pi sayısı, sıfırın icadından sonra yapılan en büyük buluştur.

Çember, insanoğlunun ilk bildiği geometrik şekillerden birisidir. Çemberi bilen eski çağ insanının, çemberin çapını, yarıçapını, çevresini ve alanını da düşünmeye başlamış olması doğaldır. Merkezi ve yarıçapı bilinen çemberin çizilebildiğini, çevre uzunluğunun ve alanının hesaplanabildiğini ilkokul sıralarından hepimiz biliriz. Kuşkusuz, bu bilgiyi, insanlar, 2000 yıldan önceki zamanlarda da bilmek istemiştir. Çapı verilen çemberin uzunluğu nedir? Çevrelediği alan nedir?

Çember, antik çağlardan beri insanoğlu için çok önemli bir geometrik şekil olma özeliğini artırarak günümüze gelmiştir. Bu gün içinde yaşadığımız bilim ve teknoloji çağının pek çok bulguları ona dayanır. Dönmenin, hareketin, tekerin içinde olduğu her olguda çember vardır. Ona ait bilgilere sahip olmasaydık, trigonometri olmazdı. Trigonometri olmayınca otomobiller yürümez, trenler gitmez, uçaklar uçmaz, santrallar enerji üretmezdi. Çember, bilim ve teknikte olduğu kadar sanatta, mimari tasarımlarda ve gündelik yaşamımızda da önemlidir.

Bu gün hepimiz çember için

ÇevreUzunluğu = π x Çap

ve

Alan = π x YarıÇap x YarıÇap

formüllerini biliriz. Bu formülleri kullanarak çevreyi ya da alanı bulabilmemiz için pi (π) sayısını bilmek gerekiyor. İki milenyumdan önceki zamanlarda da, insanlar, çapı bilinen çemberin çevre uzunluğunu ve alanını bulmak istiyorlardı. Bunları bulabilmek için π simgesi ile gösterdiğimiz katsayının bilinmesi gerekiyordu. Çevre uzunluğu formülünden

eşitliğini yazabiliriz. Bu eşitlik 2000 yıldan önceki zamanlarda da, simgesel olmasa bile kavram olarak vardı. O zamanki insanın neler düşündüğünü hayal edebilmek için, kendimizi onların yerine koyarak düşünmeye başlayabiliriz. Örneğin, bir ipi bir çember üzerine sarıp çevre uzunluğuna eşit uzunlukta bir ip elde edebiliriz. Sonra, o ipi çapa eşit bir çubukla ölçerek, çemberin çevresinin, çapının kaç katı olduğunu bulmaya çalışabiliriz. Ya da, çapı 1 birim olan çemberin çevre uzunluğunun π sayısına eşit olduğunu söyleyebiliriz. Bunu bize

ÇevreUzunluğu = π x 1 birim = π

eşitliği vermektedir. Öyleyse, üzerindeki birim uzunluk çapa eşit olacak biçimde ölçeklenmiş olan doğru bir çizgi üzerinde tam bir dönme yapana kadar çemberi yuvarlayabilir, başlangıç yerinden başlayıp gelinen yere kadar uzayan doğru parçasını ölçerek çevre uzunluğunu buluruz. Bu bize π sayısının değerini verecektir (Bkz. Şekil 1).

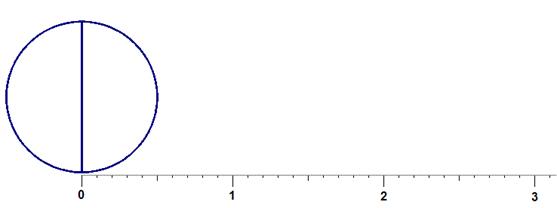
Şekil 1

Peki, yapılacak iş bu kadar kolaysa, insanoğlu neden 2000 yıl boyunca bu işle beyhude yere uğraştı? Bunun nedenini anlamak için, aynı deneyi bir kaç kez yineleyiniz. Ne kadar dikkatli davranırsanız davranın, her ölçmede farklı sonuçlar bulacaksınız. Bu sizin becerinizle ilgili değildir. Kullandığınız malzemelerin etkisi vardır, göz yanılması vardır. Doğru üzerindeki ölçekleri alt aralıklarına bölerek küçültünüz. Önceleri, skala küçüldükçe, daha doğru sonuçlar elde etmeye başlarsınız, ama milimetrenin alt katlarına inildiğinde, artık gözünüz ayrım yapamayacaktır. Bir uzunluğun ölçümü asla gerçek değeri veremez. Bu olgu, insanın ve malzemenin girdiği her ölçümde, her deneyde olur.

Aslında bu konu ölçümde yapılan hatanın ötesinde, işin özüyle ilgili derin bir konudur. Bir gün ölçüm aletleri çok gelişse, deneylerdeki ölçme hataları ortadan kalkar diye düşünebiliriz. Ama bu asla gerçekleşemez. Çünkü, irrasyonel değerleri ölçen bir alet yapılamaz. O nedenle, matematikte uzunluk, alan, hacım gibi çokluklar deneyle değil, hesapla bulunur. Hesapla bulunan ölçüm daima kesindir, gerçek değeri verir.

2000 yıl boyunca dünyanın en akıllı adamları π sayısının değerini ölçerek değil, hesapla bulmaya uğraştılar. Ama iki milenyum boyunca bulamadılar, çünkü onu olmadığı yerde arıyorlardı. Onlar yalnızca kesirli sayıları biliyorlardı; dolayısıyla π sayısının kesirli bir sayı olduğu varsayımı ile hareket ediyorlardı. Burada kesirli sayı demekle, ondalık yazılımı sonlu basamaklı olan sayıları anlıyoruz. Sonlu basamaklı ondalık sayılara devirli (periyodik) sonsuz basamaklı sayıları da eklersek rasyonel sayılar kümesini elde ederiz. Rasyonel sayılar, p ile q (q≠0) birer tamsayı olmak üzere p/q biçiminde yazılabilirler. Bu biçime uymayan sayıların varlığı çok eskiden beri biliniyordu. Örneğin birim karenin köşegeninin uzunluğu bilinen sayı tipine hiç uymuyordu. Ama bu fenomen 18. yüzyılda gerçel (real) sayıların kurulmasına kadar tam açıklanamadı. Gerçel sayıların kurulumu yapıldıktan sonra, rasyonel sayıların sayı ekseni üzerinde dolduramadıkları boşlukları dolduran irrasyonel sayıların varlığı ortaya kondu. Ondan sonra, Lambert 1766 yılında π sayısının irrasyonel bir sayı olduğunu ispatladı. Böylece, π sayısının sonlu basamaklı bir ondalık sayı ya da devirli sonsuz basamaklı bir sayı olmadığı anlaşıldı. O, sonsuz basamaklı bir sayıdır ve basamakları devirli (periyodik) değildir.

Şimdi, bulunduğumuz yerden geriye bakınca, iki milenyum boyunca dünyanın en akıllı insanlarının onu neden bulamadıklarını anlıyoruz. Ama yarışın bitmediğini ve asla bitmeyeceğini de görüyoruz. Şimdiki yarış, π sayısının daha çok basamağını bulma yarışıdır. Önce π sayısının basamak sayısını onlu katlara çıkardılar, sonra yüzlere tırmandılar. Bilgisayarlar ortaya çıkınca, milyonlara, milyarlara ulaştılar.

π sayısının ilk 100 basamağı:

3,1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679

Pek çok kişi şu soruyu soruyor: Bu günkü teknolojinin istediği duyarlığı elde etmek için, π sayısının ilk on basamağı fazlasıyla yeterlidir. Bunu şu örnekle açıklayalım. Dünyanın güneş etrafındaki yörüngesinin uzunluğunu bulmak için π yerine 3.141592654 sayısı kullanılırsa, yapılacak hata 100 metreden azdır. Dünyanın yörüngesinin uzunluğu yaklaşık 938.900.000 km dir. Kaba bir yaklaşımla söylersek, yörünge uzunluğunun hesabında yapılacak hata hemen hemen 10 milyonda 1 dir. Günümüzde hiç bir teknoloji bu yüksek duyarlığı istemez.

Matematikçi Hermann Schubert bunu daha çarpıcı bir örnekle açıklıyor. Dünyayı merkez kabul eden ve Sirus takım yıldızından geçen bir küre düşünelim. Sirus takım yıldızının bize uzaklığı 8.8 ışık yılıdır. (1 IşıkYılı, Saniyede 300 000 km yol alan ışığın bir yılda katettiği yoldur). Bu, çoğumuzun algılayamayacağı kadar çok çok büyük bir küredir. Şimdi onu daha da büyütelim. Diyelim ki bu büyük kürenin her milimetre küpü milyarlarca mikroskopik canlılarla doludur. Sonra bilinmez bir kuvvet, bütün bu canlıları uzay boşluğunda bir doğru boyunca öyle dağıtsın ki, herhangi iki mikroskobik canlı arasındaki uzaklık Sirus’un bize olan uzaklığından az olmasın. Bütün bu mikroskopik canlıları taşıyan milyar x milyar x milyar x ... IşıkYılı uzunluğundaki bu doğru parçasını çap kabul eden küreyi düşünelim. Algılamakta zorlandığımız ilk küre, bu kürenin yanında bir nokta gibi kalır.

Şimdi bu kürenin bir büyük çemberinin çevre uzunluğunu hesaplamak için 100 haneli π sayısını kullanırsak, yapacağımız hata milimetrenin milyonda birinden daha azdır.

Şimdi soruyu yeniden soralım:

Neden π sayısının daha çok basamağını bulmak için yarışıyoruz?

Buna herkesi doyuran bir yanıt veremeyiz. Ama soruyu ustaca matematikçilerin üzerinden savuşturabiliriz:

Neden insanlar Everest’e tırmanıyor?

Gelecek yazıda π sayısını bulmak için, insan aklının yarattığı harika düşüncelere gireceğiz.