Görelilik Kuramının Matematiksel Temelleri
Timur Karaçay
Başkent
Üniversitesi, Ankara
tkaracay@baskent.edu.tr
Abstract
The aim of this short talk is not to give the
rigorous mathematical foundations of relativity, since the time constraint
prevents us to do so. Instead, we shall try to explain the differences between
the mathematical tools, namely the geometries of Newtonian mechanics and
relativity for interested audience who are presumably non-experts in the field.
In classical mechanics, the one of Galileo and Newton, which deals with forces
and movements, the law of gravitation is formulated simply. From it one can
advance in two directions, which are the two types of modern physics which are
opposed to classical physics: on the one hand relativity (special then
general), on the other hand, quantum physics and statistical physics, which are
two parent theories closely related together. The mathematical foundations of
special relativity was constructed by different researchers: Poincar´e,
Lorentz, Minkowski. But the physical interpratation of this beautiful geometry
was made by Einstein. General relativity was discovered by Einstein and
Hilbert; it includes special relativity and gravitation which it interprets as
not being a force but the effect of the curvature of space-time. General
relativity and quantum theory are among the greatest intellectual achievements
of the 20th century. Each of them has profoundly altered the conceptual fabric
that underlies our understanding of the physical world. Furthermore, each has
been successful in describing the physical phenomena in its own domain to an
astonishing degree of accuracy. And yet, they are strikingly
different pictures of physical reality. Needless to say that none of the
substance of the material in these talk is new; the only reason for reading
them is if an individual reader finds the explanations here easier to
understand than those elsewhere.
Özet
Zaman elvermeyeceği için, bu konuşmada göreliliğin
sağlam matematiksel temellerini vermek amacı güdülemeyecek, onun yerine Newton
Mekaniğinde ve görelilikte matematiksel araç olarak kullanılan geometriler
arasındaki fark, konuya yabancı olanlar için açıklanacaktır. Galileo ve
Newtonun kurdukları klâsik mekanik kuvvet ve hareket arasındaki ilişkiyi
inceler ve gravitasyonu basit bir matematik formülle açıklar. Bu noktadan
sonra, fiziğin iki yöne ayrıldığını görüyoruz: Bir tarafta Görelilik Kuramı
(özel ve genel), öteki tarafta Kuantum Fiziği ve İstatistiksel Fizik. Bunlar
birbirleriyle sıkı ilişkileri olması gereken iki ana kuramdır. Özel Görelilik
Kuramının matematiksel dayanağı Poincaré, Lorentz ve Minkowski tarafından
verilmiş, bu güzel geometrinin fiziksel yorumu Einstein tarafından yapılmıştır.
Genel Görelilik Kuramı ise Einstein ve Hilbert tarafından kurulmuştur. Özel
Göreliliği içeren Genel Görelilik Kuramı gravitasyonu bir kuvvet olarak değil,
uzayzamanın eğriliği olarak açıklar. Evreni kavrayışımızı kökünden değiştiren
Görelilik ve kuantum fizikleri 20.yüzyılın en büyük bilimsel bulguları arasında
sayılmakla kalmaz, her biri kendi alanındaki fiziksel fenomenleri şaşırtıcı
duyarlıkla belirlerler, ama bir o kadar da birbirlerinden farklıdırlar.
Elbette, bu konuşmada geçen kavramların ve onların ele alınış yöntemlerinin
yeni olmadığını söylemeye gerek yoktur. Umarız ki, okurlarımız, başka yerlerden
de öğrenebilecekleri kavramları, burada daha kolay anlayacaklardır.
Giriş
Albert
Einstein Özel Görelilik Kuramını 1905 yılında ortaya koydu. Aradan geçen yüz
yılın en önemli fizik bulgusu (ya da bulgularından birisi) sayıldığı için,
Görelilik Kuramının ortaya çıkışının yüzüncü yılı Fizik Yılı ilan edildi.
Dünyanın bir çok ülkesinde üniversitelerde Görelilik Kuramını anlatan dersler,
konferanslar düzenlendi. İstanbul Kültür Üniversitesinin öncülüğünde üçüncüsü
yapılan Mantık, Matematik ve Felsefe
Sempozyumu nun bu yılki konusu, iyi bir seçimle, Görelilik Kuramına
ayrıldı.
Bu
konuşmada, Görelilik Kuramının Matematiksel Temellerini açıklamam istendi. Analiz ve Lineer Cebiri iyi bilenler için, bir sömestrelik ders olan
göreliliğin matematiksel temellerini bu konuşma metnine sığdıramayacağım
açıktır. O nedenle, görelilikte, matematiğin nerede nasıl bir araç olarak
kullanıldığını ortaya koymaya çalışacağım. Yüz yıldır her yönüyle incelenen bu
konuda bilimsel açıdan bir yenilik getiremeyeceğim apaçıktır. Başka bir
deyişle, konuşmam, konuyu bilenlere hiçbir katkıda bulunamaz. Gene de, konuyu
benden az bilen gençlere bir yol gösterebilmeyi umuyorum. Hemen belirtmekte yarar vardır. Bu gün,
matematikçiler, Görelilik Kuramını Einsteinin ortaya koyduğu yöntemle
incelemiyorlar. Aradan geçen yüz yılda göreliliği daha iyi açıklayan
matematiksel yapılar ortaya kondu. Bunların bir kısmı geometrik modeller
kullanır, bir kısmı da cebirsel modeller kullanır. Daha iyi matematiksel
modellerin ortaya çıkmış olması, Einsteinin yaptığı işin önemini azaltmaz.
Olsa olsa, Einsteinin yüz yıl önce kurduğu görkemli tiyatroda matematikçiler
iyi oyunlar sergiliyor diyebiliriz.
Genel
Görelilik Kuramı gravitasyon kuramıdır. Bu kuramın önemini anlayabilmek için,
tarih boyunca graviyasyonu insanoğlunun nasıl algıladığını bilmek gerekir. O
nedenle, Birinci Bölümde gravitasyon kavramının evrimiyle ilgili çok kısa bir
tarihçe verdikten sonra Galilei ve Newtonun ortaya koydukları Klâsik Mekaniği,
görelilik açısından ele alacağız. İkinci Bölümde Özel Göreliliği, Üçüncü
Bölümde de Genel Görelilik Kuramını açıklamaya çalışacağız.
1. Bölüm
A. Antik
Çağda Evren Modelleri
Antik
Çağda Evren Modellerini bilim tarihi açısından incelemek yerine, bizim asıl amacımız
olan Görelilik Kuramına giden yoldaki işaretler olarak ele alacağız. Dolayısıyla,
geçmişte kurgulanan önemli evren modellerine ve hareket yasalarına, kronolojik
sırada, göz atmakla yetineceğiz.
Babilliler
Fırat ve
Dicle ırmakları arasında kalan zengin topraklarda yaşayan insanlar, mezopotamya
diye anılan bu verimli yerlerde, tarih öncesi uygarlıkların en önemlilerinden
birisini kurmuşlardır. Her uygarlık gök cisimlerinin hareketini; yani evreni
merak etmiş, onu gözlemiş ve o günün olanakları içinde açıklamalar getirmiştir.
Babillilere göre, dünya büyük bir (düzlemsel) dairedir, çevresi büyük
ırmaklarla çevrilidir, bu ırmakların ötesinde aşılamaz dağlar vardır. Hiçbir
insan o ırmağı geçemez. Dağlar, çok sağlam bir maddeden yapılan gök kubbeyi bir
kemer gibi tutar. Kuzey dağları boyunca uzanan ve dış dünyaya açılan büyük bir
tünel vardır. Bu tünelin, bir ucu doğu, öteki ucu batı dağlarında olan iki
büyük kapısı vardır. Güneş hergün doğu kapısından içeri girer, batı kapısından
çıkar. Geceleri kuzey tünelde dinlenir.
Babilliler
birinci dereceden denklemleri çözebiliyordu. M.Ö. 1900-1600 yıllarına ait
olduğu belirlenen bir kil tabletinde a 2 + b2 = c2
eşitliğini sağlayan sayılar görülmüştür. Bu da gösteriyor ki, gemetrik ispatı
bilmeseler bile, Pisagor bağıntısını biliyorlardı. Bu tabletlerin sayılar
kuramıyla ilgili en eski tabletler olduğu sanılıyor. Babilliler 60 tabanlı
sayma sistemini kullanıyorlardı. Bu gün kullandığımız zaman sistemi oradan
gelir. Bir günü 24 saate, bir saati 60 dakikaya ve bir dakikayı 60 saniyeye
bölmüşlerdir. Çemberin 360 derecelik merkez açı ile ölçülmesi de onlardan
gelmektedir.
Mısırlılar
Eski
Mısırlılar dünyayı, kuzey-güney doğrultusu daha uzun olan dikdörtgensel bir
düzlem, gök kubbeyi yerden yükselen dört sütun üzerinde duran bir çatı gibi
algıladılar. Güney tarafta gök yüzünde büyük bir nehir vardır, tanrı güneş her gün bu nehirde gezintiye çıkar.
Mısırlıların
gök cisimleriyle ve matematikle ilgilenmeleri pratik bir nedene bağlıdır. Her
yıl Nil nehri taşar, ekili alanlarda sınırları yokeder. Taşma zamanını doğru
bilmek ve taşkından sonra tarlaların yokolan sınırlarını yeniden belirlemek
için gerçekçi bir takvime, yeterli matematiğe gereksemeleri vardı. Mısır
takvimi bir yılı 365 gün olarak almış ve bunu değiştirmeden yüzyıllar boyunca
kullanmıştır. Her yıl oluşan ¼ günlük
artıklar toplanınca 730 yılda, mevsimler 6 ay geriye kayar. Başka bir deyişle,
kış başlarken takvim yaz başlangıcını göstermektedir. 1460 yıl sonra, takvim gerçek mevsimlere
yeniden uyum sağlar. Bu uzun sürede, Mısırlıların takvimde düzeltme yapmayı
düşünmemiş olmaları şaşırtıcıdır.
Mısırlılar,
zamanı göstermek için su saatini icat ettiler. M.Ö.1450 yıllarına ait bir su
saati Berlin Müzesinde sergilenmektedir.
Hint
Eski Hint
uygarlığında, evren 4.32x109 yıllık
periyotlarla doğar, gelişir, çöker ve ölür. Bu oluşum, tıpkı bir farenin
doğumu, yaşaması ve ölümü gibidir ve onun kadar doğaldır.
Çin
Çinlilerin
M.Ö.1300 yıllarına kadar geriye giden astronomi gözlemleri vardır. Güneş
tutulmalarını ve 1054 yılında patlayan ve iki yıl süren supernovayı
gözleyebilmişlerdir.
Eski Yunan
Mitoloji
Eski yunan
kozmolojisi kaçınılmaz olarak mitoloji ile bağlantılıdır. Ona göre dünya
yukarıdan hava ile, çevresinden su ile ve onun altında da cehennem ile
sarılıdır. Bir süre sonra denizcilerin ticaret amacıyla yaptıkları gezilerde
Eski Mısır ve Babil uygarlıklarının kalıntılarıyla tanıştılar. Böylece, mitler
yerlerini zamanla daha gerçekçi ve mantıklı görüşlere bırakmaya başladı.
Anaxagoras (499 B.C. - 428 B.C.) Ionia doğumlu Anaxagoras, güneşin tanrı olmadığını, ayın
güneşten gelen ışınları yansıttığını savunduğu için mahküm edilmiştir. Anaxagorasın
mantıksal çıkarımlarla ulaştığı başka ilginç görüşleri vardır. Örneğin,
meteorların maddesel yapısının dünyanınki ile aynı olduğunu görmüş, sonra şu
sonuca varmıştır: Meteorlar dünyanın dönmesi esnasında dünyadan kopan
parçalardır, uzayda hızları azalınca tekrar dünyaya düşmektedirler. Bu günkü
bilgilerimizle bunun yanlışlığını biliyoruz. Ama Anaxagorasın dünyanın yuvarlaklığı,
dönmesi ve merkezkaç kuvvet gibi kavramlara o günlerde sahip olması
şaşırtıcıdır.
Miletli Tales (M.Ö. 585) Babillilerin gözlem
sonuçlarını inceleyerek güneş tutulmasını öngörmüştür. Ama o, dünyanın
okyanusta yüzdüğü, depremlerin dalgalar nedeniyle oluştuğu görüşündedir.
Democritus, sonsuz ve ölümsüz evren kavramını, Parmenides ise küresel ve hareketsiz dünya görüşünü ortaya
sürmüşlerdir.
Pisagor (M.Ö. 580) Kendi adıyla anılan felsefe okulunu kurmuştur. Matematik,
astronomi ve müzikte önemli bulgular yapan ve inanç ağırlıklı bu okul, bigileri
gizli tuttuğu için Pisagorun ürünleri tam olarak bilinmemektedir. Buna rağmen,
çok ileri bir kozmoloji geliştirdiler. Dünyanın mükemmel bir küre olduğunu, bu
şekildeki on tane gök cisminin de dünya ile birlikte merkezdeki ateş etrafında birer çember
yörüngede döndüğünü, ateşin insanlar tarafından görünemez olduğunu savunmuştur.
Bu görüş önemlidir, çünkü, gök cisimlerinin bir merkez etrafında döndüğü ilk
kez ortaya atılmış oldu. Bu evren modeli, ufak değişikliklerle 2000 yıl boyunca
ayakta kalabilmiştir.
Samoslu Aristarchus (310 B.C. - 230 B.C.) Aristarchus geometrik yolla güneşin dünyadan çok daha büyük
olduğunu kanıtladı. Sonra, böyle büyük bir cismin küçücük dünyanın etrafında
dönemeyeceği, onu dünya etrafında dönüyor gibi görünmesinin nedenini, dünyanın
kendi ekseni etrafında dönmesine bağladı. Böylece, Aristarchus, 17. yüzyılda
Copernicusun ulaşacağı heliocentric evren modelinin başlıca nedenini ortaya
koymuş oluyordu. Yazık ki bu görüşü Aristo red edecek, dolayısıyla 1800 yıllık
bir zaman kaybına yol açacaktır.
Aristo (M.Ö. 384 - 322) Aristo, kendi döneminde önem taşıyan hemen her konuda görüş
bildirmiş büyük bir düşünürdür. Mantık biliminin kurucusudur. Ortaya sürdüğü
her düşünce, bir mantık süzgecinden geçmiştir. O zamanın bilgileri ve koşulları
altında ortaya koyduğu fikirlerinin birçoğu, elbette, bu gün yanlıştır. Ama o,
2300 yıldır düşünceleriyle aramızdadır.
Örneğin,
Aristo, Dünya bir anda ortaya çıkmadı, o
her zaman vardı, ebediyen değişmeden varolacaktır der. Bu görüş, kilisenin
yaratılış
dogmasına karşıdır. O nedenle kilise önce Aristoyu dışlamak istemiş, ama onun
yüzyıllardır yayılmış fikirlerini beyinlerden silemeyeceğini anlamıştır. Bu
nedenle, kilise adamları, Aristonun düşünceleriyle kilisenin görüşlerini
bağdaştırmak için yüzyıllar süren zorlu bir çabanın içine girmiştir. Sonunda
kilise, onun tümdengelimli mantık sistemini ustaca kullanmanın yolunu
bulmuştur. Bilindiği gibi, p Þ q çıkarımında
p
nin doğruluğu ya da yanlışlığı mantığın sorunu değildir. Mantık, p önermesi geçerli ise, q önermesinin de geçerli olduğunu
söyler. Başka bir deyişle, mantık doğru düşünmenin aletidir, doğruyu bulmanın
değil! Örneğin, p yerine Dünya 7 günde yoktan yaratıldı
önermesini koyarsanız, p önermesi,
Aristonun yukarıda anılan düşüncesine ve modern fiziğin Hiçbir şey yoktan var olmaz ilkesine aykırı düşer. Ama Aristo
mantığı p önermesini geçerli sayıp
ondan sonuçlar çıkarmaya devam eder. Böylece, kilise, p öncülü (premise) yerine kendi görüşlerini koyarak istediği q vargısını elde edebilmiştir. Bu
oluşumda Aristoyu kusurlu göremeyiz. O mantık denilen güzel bir alet yarattı;
kilise o aleti kötü kullandı ve ortaçağ karanlığını yaratmayı başardı. Bu
nedenle, 17. yüzyıldan sonra modern bilimi kuranlardan bazıları, Aristoyu
kusurlu görmüşler ve tümdengelimin bilimsel bir yöntem olmadığını
savunmuşlardır. Ama, matematik tümdengelimlidir, onu yok sayarsak ortada bilim
kalmaz.
Aristonun Hareket Yasaları
- Cisimler ağırlıklarıyla orantılı
bir ivmeyle yere düşerler.
- Bir cismin hareket etmesi için
ona sürekli bir kuvvet etki etmelidir.
- F kuvveti kütlesi
m olan cismi t zamanda d uzaklığa götürüyorsa, m/2 kütleli cismi t/2
zamanda aynı d uzaklığa götürür.
- F kuvveti kütlesi
m olan cismi t zamanda d uzaklığa götürüyorsa, m/2 kütleli cismi t zamanda 2d uzaklığa
götürür.
Aristoya
göre, cismin hareket edebilmesi için bir kuvvet ona sürekli etkimelidir. Etki
edebilmesi için de, kuvvetin cisme dokunması gerekir. Sabit bir kütleye sabit
bir kuvvet sürekli etki halindeyse cisim sabit bir hızla hareket eder. Şimdi
bunların yanlış olduğunu biliyoruz. Çünkü, sabit bir kuvvetin etkisindeki cisim
ivme kazanır, dolayısıyla hızı değişir. Ama Aristonun hareket yasaları 1800
yıl boyunca varlığını sürdürdü.
Aristonun
hareket yasalarına ileride tekrar döneceğiz. Şimdilik, onun evren modelinden
sözetmekle yetinelim. Önce, dünya kendi ekseni çevresinde dönüyor diyen
Aristarchusun görüşüne karşı oluş nedenini söyleyeceğiz. Dünya kendi ekseni
etrafında dönüyor olsaydı,
- Dikey yukarı atılan bir taş aynı yere düşmezdi,
- Dünya etrafında kuvvetli bir rüzgâr oluşurdu.
Heliocentrik
(gün-merkezli) modelin doğuşunu 18 yüzyıl geciktiren bu yanlış düşüncenin, o
günkü bilgilere göre kuvvetli bir mantıksal çıkarıma dayandığını görüyoruz.
Aristonun
evren modeline gelince, 55 gök cisminin dikkatle gözlenmiş hareketlerini içeren
karmaşık bir yapıdır. Bu modele göre, gök cisimleri dünya etrafındaki küreler
üzerinde dolanırlar. Aristonun evren modelinin heliocentrik modele gidişi geciktirmiş olma gibi kötü bir ünü
vardır. Ama, model gerçek bir bilimsel çalışmanın ürünüdür. Yıldızlar dikkatle
gözlenmiş, hareketlerine ait veriler kaydedilmiştir. Bu verileri kullanarak, Aristo,
gök cisimlerinin gelecekteki hareketlerini tahmin edebilir duruma gelmiştir. Örneğin,
Mars gezegeninin bir yıl sonraki konumunu belirleyebiliyordu.
Eratosthenes (M.Ö. 276 - 197)
Şimdi Libya
içinde olan Cyrenede doğdu, İskenderiyede yaşadı. Dünyanın çevresini, bu gün
de geçerliği olan ilginç bir geometrik yöntemle ölçtü. Dünyanın bir küre
olduğunu, Mısırdaki Aswan kenti ile İskenderiye kentlerinin bir büyük çember
üzerinde (diyelim ki, aynı meridyen üzerinde) bulunduğunu ve bu çember boyunca
aralarındaki uzaklığın 5000 stadia olduğunu biliyordu. Bir çubuğun Aswandaki
gölgesi ile İskenderiyedeki gölgesi arasında yaklaşık 7.2 derece olduğunu
ölçtü. Bundan sonrası basit bir orantıyla bulunur. 7.2 derecelik merkez açıyı
gören yay uzunluğu 5000 stadia ise, 360 derecelik merkez açıyı gören tam çember
yayının uzunluğu ne olur?
Bunlardan
çıkan başka önemli bir sonuç var. Kilisenin direnmesine rağmen, dünyanın
yuvarlak olduğu (gizliden) genel kabul görmüştür. Gerçekten yüzyıllar sonra
Columbusun dünyayı dolanmak için (batıya giderek doğuya ulaşmak istiyordu)
yola çıkışı bunun iyi bir delilidir. Columbus, düz dünyanın ucuna ulaşıp aşağı
düşmekten hiç korkmadı. Onun yanlışı, büyük olasılıkla, dünya çevresini
olduğundan çok küçük tahmin etmesidir. İyi ki, yarı yolda hiç ummadığı Amerika
kıtası vardı. Yoksa Columbusun tayfaları açlık ve susuzluktan kırılabilirdi.
Batlamyus (Ptolemy (M.S. 100 - 170) Mısırda doğdu, İskenderiyede yaşadı. Büyük bir astronom ve
geometricidir. 127-141 yılları arasında astronomik gözlemler yaptı. Bulduğu
verileri Almagest adlı kitapta
topladı. Bu kitap halen astronomide güncel sayılacak değere sahiptir. Aristonun
evren modelini geliştirerek Marsın uydusunun hareketlerini epicycle adı verilen sistemle açıkladı.
Onun evren modeli 1543 yılında Copernicusun modeli ortaya çıkana kadar
yaşayacaktır.
Roma İmparatorluğu
Roma imparatorluğunun,
takvim düzenlemeleri dışında, kozmolojiye yaptığı hiçbir katkı görülmemektedir.
Ortaçağ ve Kilise
Aristonun kilise
görüşleriyle uyuşmayan görüşleri çoktur. Örneğin, 1277 yılında Paris piskoposu
Aristonun 219 doktrinini listeleyip öğretilmesini ve tartışılmasını
yasaklamıştı. Bütün bunlara rağmen, kilise Aristonun parlak düşünceleriyle
başedememiş, zamanla onların bir kısmını kilisenin resmi görüşü haline
getirmiştir.
B. Modern
Zamanlarda Evren Modelleri
Nicholas Copernicus (1473 - 1543 )
Polonyada
doğdu. Krakov Üniversitesinde matematik, astronomi ve felsefe okudu Sonra
İtalyaya gitti. Bologno Üniversitesinde liberal sanatlar, Ferrarada tıp,
Paduada hukuk eğitimi gördü. Kilise yasaları üzerine doktora derecesi aldı ve
Fraenberg kilisesinde göreve başladı. Kilise kulesinden çıplak gözle yaptığı
uzun gözlemlerden sonra, yıldızların dünya merkezli değil, güneş merkezli dairesel
yörüngeler çizdiği sonucuna vardı. Böylece, Pisagorun ortaya koyduğu
yer-merkezli (geocentric) evren modeli, tahtını 1800 yıl sonra, gün-merkezli
(heliocentric) evren modeline bıraktı. Copernicus ilk sonuçlarını 1514 yılında müsvette
olarak elden ele dolaştırdı. De
Revolutionibus Orbium Coelestium adını verdiği eseri 1543 yılında yayınlandı.
Derler ki, 1542 yılında felç geçirip yatağa düşen Copernicus, ölmeden biraz
önce kitabının ilk kopyasını görebildi.
Copernicus,
yer merkezli evren modelini yıkınca dünya güllük gülüstanlık olmadı. 1616
yılında Papa Pius V dünyanın hareketsiz durduğunu, günmerkezli sistemin kâfir
işi olduğunu açıkladı ve Copernicusun kitabını yasakladı. Kitap 1822 yılına
kadar kara listede kaldı.
Pisagordan
beri yerine oturmuş ve kimseyi rahatsız ediyor görünmeyen yermerkezli evren
modeli ortadan kalkınca, bir yandan kilisenin baskısı, öte yandan yeni modelin
belirsizliği (geleceği konusundaki endişeler), ister istemez bilimle
uğraşanları çekimser kılıyordu. Bu çekimserliğin yanında, yeni modelin
çekiciliği de kuşku götürmezdi. Kepler, Galilei ve Newton bu çekiciliğe
kendisini kaptıran ve modern bilimin oluşumuna büyük katkılarda bulunan adların
başında gelir.
Johannes Kepler (1571 - 1630)
Tübingende
okurken Copernicusun evren modeliyle tanıştı. 1596 yılında yazdığı Mysterium Cosmographicum adlı eserinde
onu savundu. 1609 yılında yayınladığı Astronomia
Novada ilk iki yasayı, 1619 yılında yayınladığı Harmonices Mundide üçüncü yasasını yayınladı. Copernicusun devrim
yaratan evren modeline son geometrik biçimi veren Keplerin gezegenlerin
hareketlerini geometrik olarak açıklayan üç yasası şöyledir:
1.
Bir gezegenin yörüngesi, bir odağında güneşin yer aldığı bir elipstir.
2.
Gezegeni güneşe birleştiren doğru eşit zamanlarda eşit alanlar süpürür.
3.
Gezegenin periyodunun karesi güneşe olan ortalama uzaklığının küpü ile orantılıdır.
Galileo Galilei (1564 -1642)
Galilei, Aristodan
beri sorulan bir soruyu tersine çevirdi: Bir
cismi düzgün doğrusal hareket ettiren şey nedir? sorusu yerine Bir cismi düzgün doğrusal hareketten
alıkoyan şey nedir? sorusunu sordu. Yaptığı deneylerle Aristonun hareket
yasalarını yıktı ve modern çağın en önemli fizik yasasını ortaya koydu:
Ağırlıklarına bağlı
olmaksızın, bütün cisimler yere aynı hızla düşerler.
Oysa,
Aristo ağır cisimlerin daha hızlı düşeceğini söylemişti. Böylece, Aristo imparatorluğu
yıkım sürecine girdi. Bu yıkım elbette acısız olamazdı. Copernicusun evren modelini savunduğu için,
Galilei, engizisyon mahkemesi tarafından sorgulandı ve yeni evren modelini
savunmaktan vazgeçmesi koşuluyla yaşam boyu ev hapsine mahkûm edildi. Ev
hapsinden kurtulamadan yaşamı sona erdi.
Galilei Göreliliği
Çok
konforlu (sarsıntısız) bir otobüsün orta sıralarında gözleriniz kapalı
gidiyorsunuz. Yol, otobüste hiçbir sarsıntı yaratmayacak pürüzsüz bir asfalt
kaplamaya sahip olsun. Şoför sabit bir hızla doğrusal bir hatta (ivmesiz)
giderken, otobüsün hareketini algılayamazsınız. Ama, dönemeçlerde otobüsün
dönüşünü, tepeüstlerine çıkışını ve vadilere inişini algılarsınız. Benzer
olarak, şoför fren yaparak hızı azaltırken ya da gaza basarak hızı artırırken
hareketi algılarsınız. Çünkü, bu durumlarda otobüs ivmeli hareket halindedir. Şimdi
bunu başka bir biçimde ifade edelim.
Sakin (hiç
dalgasız) bir gölde düzgün doğrusal hareket eden (ivmesiz hareket) bir gemide
penceresiz bir odadaki bir gözlemci ile, gölün kıyısında penceresiz bir evde
oturan başka bir gözlemci düşünelim. Her iki gözlemcimiz istedikleri mekanik
deneyleri yapabilecek aletlere (sarkaç, top, ip, cetvel vb.) sahip olsunlar. Şimdi
şu üç soruya yanıt arayalım:
1.
Gölün
kıyısındaki gözlemci, yapacağı mekanik deneylerle göldeki geminin, gölün
kıyısına göre, hareket ettiğini belirleyebilir mi?
2.
Gemideki
gözlemci, geminin gölün kıyısına göre, hareket ettiğini belirleyebilir mi?
3.
İki
gözlemcinin yapacağı mekanik benzer deneylerin sonuçları farklı mıdır?
Bu soruların
her üçünün de yanıtları hayır olacaktır. Gölün kıyısında her yanı
kapalı evde oturan gözlemcinin gölde hareket eden gemiyi algılaması
olanaksızdır. Gemi düzgün doğrusal hareket ettiği için, gemideki gözlemcimiz de
kamarasında geminin hareketini algılayamaz. Başka bir deyişle, her iki
gözlemcinin yapacağı mekanik deneyler, geminin hareketine ait bir algılama
yapamaz. Kapalı kamarada yapılan bütün mekanik deneyler, gölün kıyısındaki evde
yapılacak benzer deneylerle aynı sonucu verir.
Dolayısıyla,
geminin içinde yapılan deneylerle, kıyıdaki evde yapılan deneylerin mukayesesi
de geminin hareketine dair bir ipucu veremez. Geminin kıyıya göre hareket
ettiğini belirleyebilmek için gemideki gözlemci kamaradan çıkıp kıyıyı
gözlemelidir. Benzer şekilde, kıyıdaki gözlemci de gemiyi gözlemelidir.
Bu
söylediklerimiz, geminin düzgün doğrusal hareketi (ivmesiz hareket) için
geçerlidir. Gemi hızını artırsa, yavaşlatsa, sağa ya da sola dönse kapalı
kamaradaki yolcu o hareketleri hissedecektir. Mekanik deneyler de bunu
algılayabilecektir. Başka bir deyişle, gemi ivmeli bir hareket yaptığında
gemideki gözlemci (ya da mekanik deneyler) bu hareketi anında algılayabilir.
Ama, bu
durumda, kıyıdaki gözlemci bu hareketleri algılayamaz. Gemi ivmeli hareket
yaparken, gemideki deney sonuçları ile kıyıdaki deney sonuçları birbirinden
farklı olacaktır.
Galilei,
bu gözleminin sonucunu şu görelilik postülatı ile veriyor:
Birbirlerine göre sabit hız ve
doğrultuda hareket eden iki gözlemci bütün mekanik deneylerde aynı sonucu elde
ederler.
Konuşlanma
Sistemleri (Konaç Dizgeleri - Frames of
Reference)
Şimdi
başka bir gözlem yapalım. Uzayda nesneleri birer nokta gibi düşünelim. Analitik
geometriden bildiğimiz gibi, üç boyutlu uzayda nesneleri (noktaları) (x,y,z) ile, xy-düzlemindeki nesneleri (x,y)
ile, Ox-ekseni üzerindeki nesneleri x ile ve O(0,0) başlangıç noktasını O
ile gösterelim. Simetri ekseni Oz-ekseni
olan bir burgu yüzeyi (helicoid) üzerinde ve burgu yüzeyinin eksene en uzak
noktalarının oluşturduğu eğri üzerinde sabit bir hızla yukarı çıkan bir böcek
varolsun. A,B,C,D gözlemcileri
böceğin burgu üzerindeki hareketini gözlüyor. Varsayalım ki A gözlemcisi üç boyutu algılıyor, B gözlemcisi yalnızca xy-düzlemindeki cisimleri algılıyor, C gözlemcisi yalnızca Ox-ekseni üzerindeki cisimleri
algılıyor, D gözlemcisi ise yalnızca O(0,0) noktasındaki cisimleri algılıyor.
Bu dört gözlemcimiz, gözlem sonuçlarını rapor ederlerse, şunları yazacaklardır:
A gözlemcisi: Böcek
sabit hızla burgunun dış kenar çizgisini takip ederek yukarı doğru
tırmanıyor.
B gözlemcisi: Böcek
xy-düzleminde bir daire üzerinde
sabit bir hızla dönüyor.
C gözlemcisi: Böcek,
Ox-ekseni üzerinde [-1,+1] aralığında, bir uçtan ötekine
sabit bir hızla gidip geliyor.
D gözlemcisi: Böcek
O noktasında hareketsiz duruyor.
Görüldüğü
gibi, aynı hareketi, dört gözlemci çok farklı biçimlerde algılamaktadır. Bunun
nedeni, gözlemcilerin algılama yetenekleridir. Bunu, matematik diliyle
söylersek, gözlemcilerin kullandıkları koordinat sistemleri algılamalarını etkilemektedir.
Lise bilgilerimize göre, koordinat sistemi, uzayda, bir cismin (noktanın)
konumunu belirtir. Ama, hareket söz konusu olunca işin içine zaman da
girecektir. Bir cismin hareketini belirleyebilmek için onun ne zaman, nerede olduğunu
bilebilmemiz gerekir. Nerede olduğunu söyleyebilmek için bir koordinat
sistemine gerekseme vardır. Koordinat sisteminde hareketli bir cismin hangi zamanda nerede bulunduğunu
söyleyebilmek için de bir saat'e
gereksememiz vardır. Burada saat sözcüğü, zamanı ölçen bir boyut gibi
düşünülebilir. Aslında, bu görelilik kuramını doğuran zor bir kavramdır. Ama,
şimdilik, işe zamanı da bir boyut olarak katarak şu tanımı yapabiliriz:
Bir konuşlanma sistemi (konaç dizgesi
frame of reference), bir başvuru (reference) noktasına göre bir nesnenin ne zaman, nerede bulunduğunu belirleyen araçtır.
Bu tanım,
aslında (x,y,z) ile gösterdiğimiz
konumları, t zamanı göstermek üzere, (t,x,y,z)
biçiminde göstermek demektir. Tabii, üç boyut yerine iki ya da bir boyutlu
hareketleri de düşünebiliriz. O zaman (t,x,y,z) yerine (t,x,y) ya da (t,x) alabiliriz. Bu tür konuşlanma sistemlerine
Galilei koordinat sistemi ya da kısaca Galilei sistemi diyeceğiz.
Mutlak
Uzay, Mutlak Zaman
Asıl konumuz olan Görelilik Kuramının
neden doğduğunu açıklayabilmek için, Newtonun hareket yasalarının gerisinde
yatan düşünceyi biraz açmakta yarar vardır. Newtona göre bütün hareketlerin
içinde oluştuğu bir mutlak uzay vardır, o bize bir olayın nerede
olduğunu belirtir. Mutlak uzay hareketsizdir, daima olduğu gibi kalır, kendi
dışındaki her şeyden bağımsızdır. Mutlak uzayda yer belirleyebilmemiz için mutlak uzaklık
olması gerektiği sonucu çıkar. Ayrıca, uzaydan bağımsız bir mutlak zaman vardır, o da bize olayın ne zaman olduğunu belirtir.
Newton Mekaniğinin geometrik aracı olan
Galilei koordinat sisteminde uzay ve zaman mutlaktır ve birbirlerinden ayrı olarak
düşünülürler. Orada hareketi doğru, düzlem ya da 3-boyutlu uzayda
düşünebiliriz. Hareket denklemlerinde zamanı uzayın diğer koordinatlarından tamamen
bağımsız bir parametre (değişken) olarak düşünürüz. Bu nedenle, hareketin
yörüngesini y=f(x), x=(x1,x2,x3),
xi=xi(t), (i=1,2,3) gibi bir fonksiyonla belirleriz.
Bu durumda dy/dt hareketin hızını,
d2y/dt2 ise ivmesini
verir. Tersine olarak, ivmesi bilinen ve belli bir noktadan (başlangıç koşulu) geçen düzgün
hareketli bir cismin yörüngesini belirleyebiliriz. Görüldüğü gibi, Galilei
sisteminde (Newton mekaniğinde) hareketi incelemek için 4-boyutlu uzayı bir
araç olarak kullanmamız gerekmiyor. Uzayı belirleyen koordinatlarda mutlak
zamanı parametre olarak kullanmak yeterli oluyor. Ama, görelilik kuramında
işimize yarayacak görsel bir açıklama getirmek istersek, şöyle bir düzenek
düşünebiliriz. Cismin düzlemde hareket ettiğini varsayalım. Ox, Oy ve Ot doğruları başlangıcı O
noktasında olan bir kartezyen koordinat sistemi oluştursun. Bu sistem, bir
Galilei uzay ve zaman
sistemidir. xy-düzleminde hareket
eden bir cismin t=0 anında O(0,0) dan başladığını ve t=T anında düzlemde bir P(x,y) noktasına geldiğini varsayalım. xy-düzlemini kendisine paralel olarak Ot-ekseni boyunca T kadar kaydırırsak, P
nin yeni konumunun 3-boyutlu uzayda P1(T,x,y)
olduğunu görebiliriz. Buradan
anlaşıldığı gibi, Galilei sisteminde (Newton mekaniğinde) uzayı ve zamanı
birbirinden ayrı tutabiliyoruz. Bu ayrımı belirtmek için, uzay ve zaman sözcükleri
arasına (ve) koyarak uzay ve zaman biçiminde yazacağız. Görelilik kuramında ise mutlak uzay ve mutlak zaman
olmadığını göreceğiz. O nedenle, uzayı ve zamanı birbirlerinden ayıramayacağız.
İkisi arasında ileride açıklayacağımız farkı belirtmek için, görelilikte
kullandığımız sistemi uzayzaman biçiminde bitişik yazacağız.
Buraya kadar söylediklerimizi özetleyelim. Cismin
uzayda (doğru, düzlem ya da 3-boyutlu olabilir) yerini belirtecek bir koordinat
sistemine ek olarak zamanı belirtecek bir boyut (saat) eklediğimizde bir konuşlanma sistemi (konaç
sistemi, referans sistemi, frame of reference) elde ederiz.
Olay
Uzayzamanda bir andaki oluşuma olay diyeceğiz. Örneğin, bir topun
atılması, bir camın kırılması, bir yıldızın patlaması gibi süreci olmayan (oluş
süresi sıfır olan) anlık hareketlerdir. O nedenle, uzayzamanda bir olayı (t,x)
biçiminde bir nokta ile göstereceğiz. Bu gösterimde t zamanı, x uzayı
belirtecektir. Zaman gösteren t
değişkeni 1-boyutludur, uzayı gösteren x değişkeni 3-boyutludur. Dolayısıyla
4-boyutlu bir uzayda çalışacağız. Ama algılamayı ve çizenekleri kolaylaştırmak
için çoğunlukla konuşlanma sisteminde uzayı gösteren x değişkeninin boyutunu 1 ya da 2 olarak alabiliriz.
Uzaklık (metrik)
Hareketi incelemek için uzaklık kavramı gereklidir. Öklit uzayında A(x1,y1,z1)
ile B(x2,y2,z2)
noktaları arasındaki uzaklık Pisagor bağıntısından elde edilen
|AB|2 = (x2-x1)2
+ (y2-y1) 2 + (z2-z1)
2 (1)
bağıntısı ile verilir. Öklit Metriği dediğimiz bu
fonksiyon zamandan bağımsızdır ve Öklit Geometrisine uyumludur. Örneğin, negatif değer almaz, üçgen
eşitsizliğini sağlar, A ile B arasındaki bütün yollar arasında en kısa
olanıdır.
Yakın çevremizde ışık hızından çok çok küçük hareketleri
(yavaş hareketleri) incelerken Öklit Geometrisi ve Öklit Metriği yeterlidir.
Ama hızı ışık hızına yaklaşan hareketler için Öklit Geometrisi yerine başka
geometrileri kullanmak gerekmektedir. Bu geometrilerin kendilerine özgü
metrikleri (uzaklıkları) vardır. Bunlardan birisi olan Minkowski Metriğini ileride ele
alacağız.
Hız
Şimdi
gemiyi tekrar düşünelim. Geminin sabit varsaydığımız hızı ancak bir başvuru sistemine
göre belirtilebilir. Farklı başvuru
noktaları için, farklı hızlar ortaya çıkar. Örneğin, geminin içerdeki
gözlemciye göre hızı 0 iken, kıyıdaki eve göre 0 dan farklıdır. Aynı geminin,
sahil yolunda hızla giden bir spor otomobile göre hızı, yukarıdakilerin her ikisinden
de farklı olacaktır. Bundan çok önemli
bir fiziksel sonuç çıkar:
Hız mutlak değildir.
Bu sonuç Einsteinin
Görelilik Kuramına giden yoldaki önemli kilometre taşlarından birisidir.
Isaac Newton (1643-1727)
1. Hareketli bir cisim dışarıdan bir
kuvvetle etkilenmezse düzgün doğrusal hareketini ilelebet sürdürür.
2. Kütlesi m olan bir cisme uygulanan F kuvveti ile a ivmesi arasında F=ma bağıntısı vardır.
3. Her etkiye karşı ona eşit bir tepki
vardır.
M ile m iki cismin kütleleri, r
aralarındaki uzaklık, G gravitasyon
katsayısı olmak üzere, iki cisim arasındaki F
çekim kuvveti
F = G mM / r 2
bağıntısıyla verilir. Euler, Newton
gravitasyon yasasının analitik biçimini verdikten sonra Lagrange, Hamilton,
Jacobi, Clairaut, Laplace ve Poisson gibi ünlü matematikçiler, gravitasyon
yasasının matematilsel temellerini sağlamlaştıran teoremleri kurdular. Bu arada
potansiyel gibi yeni kavramları da ortaya çıkardılar. 20.yüzyıl başlayana dek,
hareketle ilgili her şeyin Newtonun hareket yasalarıyla hesaplanabileceği
inancı yerleşik kalacaktır. Newton Mekaniği ya da klâsik
mekanik denilen ve teknikte muazzam bir uygulama alanı bulan bu
yasaların uygulanamadığı durumlar şunlardır:
1.
10-8 cm den küçük uzaklıklar.
2.
Gravitasyonu güneşe göre 108 kat daha büyük olan cisimler.
3.
Hızı 108
m/sn den büyük olan cisimler.
Newton Mekaniğinin geçerli olmadığı
yerlerde Kuantum Mekaniği ve Einstein Mekaniği kullanılır. Kuantum Mekaniği
atomaltı parçacıkların hareketlerini belirlemek için, Einstein Mekaniği ise
hızı ışık hızına yakın büyük gök cisimlerinin hareketlerini açıklamak için
kullanılır. Elbette bu üç mekaniği içine alan bir mekanik kuram
yaratılabileceği inancını her fizikçi taşır.
Eylemsizlik
Kütlesi, Gravitasyon Kütlesi
Newtonun ikinci yasasını F = mia ile, iki cisim arasındaki çekim kuvvetini
belirten denklemi de ![]() biçiminde
yazalım. Bu iki denklemdeki mi ve mg nicelikleri fizik tarihi bakımından önemlidir.
biçiminde
yazalım. Bu iki denklemdeki mi ve mg nicelikleri fizik tarihi bakımından önemlidir.
Birincideki mi niceliğini, cismin F kuvveti etkisinde kalarak a
ivmesiyle hareket etmesine karşı koyuşun (etki-tepki) bir ölçüsü olarak
görebiliriz. mi sabit tutulduğunda, a ivmesinin artması için F
kuvveti artmalıdır. Benzer şekilde, a sabit tutulduğunda, mi niceliği büyüdükçe F kuvveti artar. Bu özelik
nedeniyle F = mia eşitliğindeki
mi niceliğine eylemsizlik kütlesi (inertial mass) denir.
İkinci
eşitlikteki mg niceliği ise Fgrav
gravitasyon kuvveti ile doğru orantılıdır; mg büyüdükçe Fgrav
artar. Bu niteliği nedeniyle,
bu eşitlikteki mg niceliğine gravitasyon kütlesi (gravitational mass) denir.
Newton Mekaniğinde, bu iki kütle, cismin
farklı özelliklerini belirtir ve kuramsal açıdan birbirlerine eşit olmak
zorunda değildir. Galileiden sonra Huygens, Newton, Bessel ve daha başkaları mi ile mg arasındaki farkı ortaya çıkaracak ölçümler
yaptılar. Ama bir cismin eylemsizlik kütlesinin gravitasyon kütlesinden farkını
ölçemediler, hesaplayamadılar, 20.yüzyıl başlarında, Baron von Eötvös tahta ve
platin gibi farklı maddelerle, 109
da 1 duyarlılıkla yaptığı
ölçümler sonunda mi ile mg arasında bir fark bulamadı. 1950/60
yıllarında R.Dicke tarafından bu ölçümler 1011 de 1 duyarlılıkla tekrarlandı,
ama bir fark görülemedi.
Pratikte hesaplanamayan, ama klâsik
mekanikte kuramsal olarak var görünen mi ile mg arasındaki farkı, Newton, doğanın bir
niteliği olarak kabul etmiştir. Ama, Einstein, bu farkın bulunamayışını,
görelilik kuramına giden yoldaki kilometre taşlarından bir başkası olarak
yorumlayacaktır.
Galilei
Yasasının Matematiksel Kanıtı
Şimdi M
kütlesi olarak dünyayı alalım ve m
kütlesinin Fgrav gravitasyonu etkisiyle dünya
merkezine doğru, a ivmesiyle
çekildiğini varsayalım. Bu durumda,
![]()
eşitliğini kurabiliriz. Şimdi ortadaki eşitlikte m leri sadeleştirirsek a = MG/r2 eşitliği çıkar. Bu da gösteriyor
ki, m
kütlesinin dünya (M) tarafından
çekilmesi esnasında doğan a ivmesi çekilen m kütlesine bağlı değildir. Bu sonuç, Galileinin gözlemle ulaştığı
Bütün cisimler aynı ivmeyle yere düşerler.
diyen yasasının matematiksel kanıtıdır.
Eylemsiz Konuşlanma
Sistemleri (Inertial Frames)
Fizik derslerinde öğrendiklerimizin
aksine, iki yüz yıl boyunca bilimin ve teknolojinin temeli olan Newton
'un eylemsizlik yasası mutlak doğru
değildir. Bu yasanın doğruluğu, hangi konuşlanma sistemine göre konuştuğumuza
bağlıdır. Buna örnekler verebiliriz:
·
Koordinat sisteminin merkezi ile cismin kütle merkezi
çakışık iseler, cisim nasıl hareket ederse etsin, sözkonusu koordinat sistemine
göre hareketsizdir.
·
Yerküre çevresinde hızla dönen bir uzay gemisindeki
kumanda masası, gemiye göre, hareketsizdir; ama o gravitasyonun ve gemiyi
yörüngede döndüren kuvvetin etkisi altındadır ve gemi dışındaki bir gözlemciye
göre hareketlidir.
·
Bir arabanın boş bagajına konulmuş bir top düşünelim.
Araba hızlanırken, top bagajda geriye doğru, araba fren yaparak yavaşlarken
ileriye doğru yuvarlanır. Oysa bagajdaki topa etki
O halde, ne zaman Newton'un eylemsizlik
yasasından sözediyorsak, o yasanın geçerli olduğu bir konuşlanma sistemine göre
konuşuyoruz demektir. Bu tür konuşlanma sistemlerine Eylemsiz
Konuşlanma Sistemleri diyeceğiz. Başka bir deyişle, bir Eylemsiz
Konuşlanma Sistemi ivmesiz bir koordinat
sistemidir. Dolayısıyla, bir eylemsiz koordinat sistemi, bir
referans noktasına göre sabittir ya da düzgün doğrusal hareket eder.
Böyle sistemlerin var olup
olmadıkları düşünülebilir. Şimdilik, şunu söylemekle yetineceğiz. Bir eylemsiz
konuşlanma sistemi varsa, sonsuz tane eylemsiz konuşlanma sistemi kurulabilir.
Gerçekten, birinci sisteme göre düzgün doğrusal hareket
Eylemli Konuşlanma
Sistemleri
İçinde eylemsizlik
yasasının geçerli olmadığı konuşlanma sistemlerine eylemli konuşlanma sistemleri
(Noninertial Frames) denilir. Bu sistemler, eylemsiz sistemlere göre bir
ivmeye sahip sistemlerdir.
Galilei
Görelilik İlkesi
K ve K'
iki eylemsiz konuşlanma sistemi olsun ve K' sistemi K
ya göre sabit v hızıyla Ox
doğrultusunda hareket etsin. Bir P
noktasının bu iki sisteme göre konaçları (koordinatları), sırasıyla, (x,t)
ve (x',t') olsun. Bu konaçlar arasında
x' = x - vt ,
t' = t
bağıntısı vardır. Burada, her iki
sistemde zaman koordinatlarının (saatlerin) aynı olduğunu varsayıyoruz (t =
t'). K sistemi içindeki bir gözlemciye göre bir t anında bir
cismin yatay eksendeki konumu x = x' + vt dir. K' sistemi
içindeki bir gözlemciye göre ise aynı t = t'
anında cismin yatay eksendeki konumu x' dür. Yukarıdaki
bağıntıdan
x = x' + vt , t = t'
yazabiliriz. Galilei
dönüşümü denilen bu bağıntıları kullanarak, cismin bir eylemsiz
sistemdeki konumunu biliyorsak, öteki sistemdeki konumunu daima bulabiliriz.
Eylemsiz Sistemlerde
Fizik Yasaları
Bu konuşma boyunca fizik yasaları, hareket yasaları ve mekanik yasaları deyimlerini eşanlamlı olarak kullanıyor olacağız.
Eylemsiz sistemlerde fizik yasaları aynıdır. Daha açık söylemek gerekirse,
birisi ötekine göre düzgün doğrusal hareket eden iki eylemsiz sistemin
birisinde geçerli olan fizik kuralları diğerinde de aynen
geçerlidir. Dolayısıyla, bir eylemsiz sistemin ötekine üstünlüğü yoktur.
Bu özelik, fizik yasaları için istediğimiz eylemsiz konuşlanma sistemini
seçebileceğimiz anlamına gelir.
Galilei dönüşümlerini kullanarak, K
ve K sistemleri için hareketin yörüngesini (yol)
ayrı ayrı yazabiliriz:
x = x(t) = x' + vt
ve x' = x' (t) = x
vt
Her iki yolun t zamanına göre ikinci türevleri hareketin K ve K sistemleri içindeki
ivmesini verecektir. Bunu yapınca d2x/dt2 = d2x/dt2 çıkar. Demek ki, her iki sistemde ivmeler
birbirlerine eşittir. Düzgün bir hareketi kendi ivmesi belirlediğine göre, K ve K sistemlerinde hareket
yasaları aynıdır. Dolayısıyla, Galilei dönüşümlerinden, Galilei Görelilik İlkesi denilen şu
önemli sonuç çıkar:
"Fizik yasaları Galilei dönüşümü altında
değişmezler."
Bunu başka biçimde de ifade edebiliriz:
Fizik yasaları bütün eylemsiz sistemlerde aynıdır.
Hızların
Toplanması Kuralı: Galilei Görelilik İlkesi şu kuralı doğurur: v hızıyla giden bir arabadan u
hızıyla bir cisim ileriye doğru atılırsa, cismin hızı arabadaki gözlemciye göre
u, yerdeki gözlemciye göre u+v dir. Arabadan daha hızlı giden bir
motosikletin hızı w ise, motosikletteki gözlemciye göre cismin
hızı (wv)+u dur. Buna hızların toplanması
kuralı diyoruz.
Eylemli
(ivmeli) Sistemlerde Fizik Kuralları
Eylemli sistemlerde Newton'un ikinci hareket yasası
geçersizdir.
Uzayda yerküre etrafında dönen bir uzay
gemisini düşünelim. Gravitasyon gemiye ve gemi içindeki her şeye etki eder, ama
gemi içindeki hiç bir cisim gemiye göre ivme kazanamaz. Bu duruma ağırlıksız ortam denir. Ağırlıksız ortam gravitasyonsuz ortam demek değildir.
İşin aslına bakarsak, gravitasyonsuz olsa, uzay gemisi dünya etrafındaki
yörüngesinde duramaz, uzaklaşırdı. Gerçekte olan şey şudur: Uzay gemisi ve
içindeki her şey dünya merkezine doğru devamlı düşme halindedirler.
Fizik derslerinden anımsayacağınız gibi,
(hayali) bir merkezkaç kuvvet uygulayarak
eylemli sistemlerde de F = ma yasasını geçerli
kılabiliriz. Merkezkaç gibi hayali kuvvetlere eylemsizlik
kuvvetleri diyoruz. Eylemsizlik kuvvetleri, cisme ivme kazandırmaya
çalışan kuvvet(ler)e karşı duran kuvvet(ler)dir.
Şimdilik, eylemsiz
ve eylemli sistemlerde fizik yasalarının
farklı uygulanacağını bilmemiz yetecektir.
Newton hareket yasaları bir teknolojik
uygarlık yaratmış olmakla beraber, ışık hızına yakın hızlarda hareket eden
cisimlere uygulanamadığı ortaya çıkmaya başladı.
İkinci Bölüm
Talihsiz bir Adlandırma:
Relativity
Bazen büyük bilimsel bulgulara, o buluşun anlamını
saptıracak talihsiz adlar verilir.
Görelilik de bunlardan biridir. Her
şey görelidir deyince, Einsteinin büyük hayali çoğunlukla yanlış
anlaşılıyor. Sanki ortada doğru bir
şey yok, herkes kendi bakış açısını doğru
imiş gibi ortaya sürmekte özgürdür gibisine yanlış bir izlenim doğuyor. Oysa
Einstein, bunun tam tersini yaptı. O fizik kurallarının evrenselliğini, bakış
açısına göre değişmezliğini gösterdi.
Önceki bölümde anlatıldığı gibi, görelilik kavramının
doğuşu Einsteindan çok öncedir. En azından Galileiye kadar geriye
götürebiliriz. Newton, görelilik kavramını bilinçle kullanmış ve hareket
yasalarını mutlak
uzay ve mutlak zamana göre ifade etmiştir. Einsteinin
özel görelilik kuramının Galilei ve Newton göreliliğinden farkı, uzayın ve
zamanın mutlak olamayacağını söylemesidir. Matematiksel açıdan bakınca, Galilei
dönüşümleri yerine Lorentz dönüşümünü kullanması ve çıkan sonuca yepyeni bir
fiziksel yorum getirmesidir. Tabii, şimdi basitçe ifade ettiğimiz bu iş, o gün
için hayal edilmesi zordu ve Einsteinin bu büyük hayali 20. yüzyıl başlarında
fiziğe bakışımızı bütünüyle değiştiren büyük bir bilimsel bulgudur.
Konuya girmeden önce, kısaca söylemek gerekirse, Özel Görelilik kuramı, fizik yasalarının
eylemsiz konuşlanma sistemlerinde aynı olduğunu söyler. Genel Görelilik Kuramı ise, bunu genelleştirir ve fizik yasalarının
eylemli sistemlerde de aynı olduğunu söyler. Elbette, bu basit yargılar ortaya
büyük fiziksel sonuçlar çıkardı. Bu ve bundan sonraki bölümde, o sonuçların
bazısına değinebileceğiz.
Özel Görelilik Kuramı
Newton Mekaniği 200 yıldan fazla bir süre fiziksel
bilimlerin harika bir aracı oldu. Ona dayalı bir bilim ve teknoloji çağı
yaratıldı. Halen bu çağın harikulade nimetlerinden yararlanıyoruz. Ama
fizikçiler daha 19.yüzyıla girilirken, Newton Mekaniğinin bazı doğa olaylarını
açıklamakta yetersiz kaldığını sezmeye başlamışlardı. Nitekim, 1884 yılında
Lord Kelvin Baltimore konferanslarında Fizik
üzerinde dolaşan 19.yy bulutları ndan sözediyordu. Newton Mekaniğinin açıklayamadığı
doğa olaylarından bazılarını sıralayabiliriz:
1.
Işığın
bir dalga hareketiyle yayıldığı genel kabul görmüştü, ama o dalgayı taşıdığı
varsayılan ve uzayı dolduran ortamın (ether) var olduğunun kabul edilmesi
çelişki yaratıyordu (Michelson-Morley deneyi).
2.
Maxwellin
Elektrik ve Magnetizma denklemleri Newton Mekaniğinin temeli olan mutlak uzay ve mutlak zaman kavramlarıyla çelişiyordu.
3.
Newton
hareket yasalarıyla Merkür
gezegeninin yörüngesi çok büyük bir duyarlılıkla hesaplanabiliyordu. Ancak,
gözlem sonuçlarıyla hesap sonuçları arasında beliren küçük ama rahatsız edici
bir fark ortaya çıkıyor, ama nedeni açıklanamıyordu.
4.
Çok
düşük ısıdaki maddeler Newton yasalarına göre hareket etmiyordu.
5.
Newton
fiziğine göre, sabit ısıdaki bir ocağın sonsuz enerjisi olmalıydı.
Bu ve benzeri sorunların giderilebilmesi için
fizikçiler çok uğraştılar, ama sonuç alamadılar. Sonuç çıkmamasını bu gün doğal
karşılıyoruz, çünkü mutlak uzay ve mutlak zaman kavramlarına dayalı
çözüm getirilemezdi. Başka bir deyişle, ortaya çıkan sorunların Newton Mekaniği
ile çözülebilmesi olanaksızdı.
Çözüm yönünde ilk doğru adımı Lorentz attı. İkinci
önemli adım ise, zamanın ünlü matematikçisi Poincareden geldi. Bu ikisi,
birbirlerinden bağımsız olarak, Görelilik Kuramı için gerekli bütün
matematiksel araçları ortaya koymuşlardı. Ama onlar ortaya koydukları
matematiksel formüllere fiziksel anlam veremediler.
Onları yorumlayıp, evrene bakışımızı değiştiren kuramı
ortaya atan Albert Einstein oldu. 1905 yılında Özel Görelilik kuramını ortaya
koydu. Bu kuramda Einstein, fizik yasalarının bütün eylemsiz sistemlerde aynı
olduğunu gösterdi. Ama bu önemli sonuç onun için yeterli değildi. Fizik
yasaları evrensel ise, eylemsiz sistemlerde olduğu gibi, eylemli sistemlerde de
aynı olmalıydı. Bunun için gravitasyonu
yaratan nedeni bulması gerekiyordu. Bunu bulması tam 10 yılını aldı. 1915
yılında da Genel
Görelilik kuramını ortaya koydu. Bu iş, 1800 yıllık Aristo evren
modelini 1543 yılında Copernicusun yıkışından çok daha görkemli oldu.
Şimdi, Özel Görelilik Kuramının zor olmayan
matematiksel dayanaklarını ortaya koyabiliriz. Bunun için, öncelikle, görelilik
kuramına giden yolu açan nedenleri ve onları açıklamakta kullanacağımız
araçları anlamalıyız.
Maxwell Newtona Karşı
James C. Maxwell (1831-1879)den önce, Gauss, Ampere
ve Faraday elektrik ve magnetizma konusunda epey ilerleme kaydetmişlerdi. Ama
bu iki kuram birbirinden farklı iki konu olarak algılanıyordu. Maxwell,
elektromagnetik dalgaların varlığını gördü ve bunların hızlarını buldu.
Elektrik ve magnetizma arasındaki ilişkileri kuran Maxwell denklemleri elektrik
ve Magnetizma kuramlarını bireştirdi. Elektromagnetik dalgaların ışık hızıyla
yayıldığını, başka bir deyişle, ışığın elektromanyetik dalgalar halinde
yayıldığını ortaya koydu. Bu hızın elektrik
ve magnetizma alanlarından tamamen bağımsız bir sabit olduğunu
belirledi. Böylece evrensel bir sabiti, ışık hızını, keşfetmiş oluyordu. [Çok duyarlı deneylerle, ışık hızı c=3x108 m/sn
(yaklaşık 300 000 km/sn) olarak ölçülmüştür.]
Maxwell denklemleri kendi başlarına çok
önemlidirler, ama ondan daha önemlisi görelilik kuramının doğuşuna yol açmış
olmalarıdır. Maxwell denklemleri fizikte çözülmesi gereken önemli bir sorun
yarattı. Bu sorunun ortaya çıkması, 20. yüzyıl başlarında fizik yasalarına
bakışımızı tümüyle değiştiren bir olgu oldu. Bilim tarihine baktığımızda
görüyoruz ki, ortaya bir sorunun çıkması
ve onun çözümü için uğraşılması, bilimsel sıçramaların nedeni olmuştur. Maxwell denklemleri de bunlardan birisidir.
Galileinin Görelilik İlkesi fizik
yasalarının her eylemsiz sistemde aynı olduğunu söylüyor. Bunu ışık hızı için
yorumlarsak, ışık hızının mutlak olamayacağı, gözlemcinin ve ışık kaynağının
içinde bulundukları sistemlere göre değişeceği anlamına gelir. Yukarıda anılan
Galilei dönüşümü uyarınca, yerdeki bir gözlemci, v
hızıyla hareket eden bir kaynaktan çıkan ışığın hızını v+c
olarak görmelidir (hızların toplamı
ilkesi). Öte yandan, Maxwell ışık hızının her gözlemciye göre sabit ve
sonlu bir değerde olduğunu söylüyor. O halde, Maxwelle göre, bütün gözlemciler
ışık hızını c olarak görecektir. Zaten
deneyler de bunu gösteriyor. Eğer ışık hızı sonsuz olsaydı, Maxwellin bulduğu
sonuç Galileinin uzay ve zaman sistemi ile çelişmezdi. Ama, Maxwell
ışık hızına denk olan elektromagnetik dalgaların hızının sonlu ve sabit
olduğunu belirlemişti. Sorunun çözümü için fizikçiler işe koyuldu.
Ether denen
şey!
1.
Işık elektromagnetik dalgalar biçiminde yayılıyorsa, bu
dalgaların oluştuğu bir ortam olmalıydı. En geçerli görünen görüş ether
kuramıydı. Ses dalgalarının yayılabilmesi için hava, su vb. bir ortamın olması
nasıl gerekiyorsa, ışık dalgalarının da boşlukta yayılabilmesi için bir ortama
gereksinimi var olmalıydı. Bütün uzay boşluğunu doldurduğu varsayılan bu
maddeye ether
denildi.
2.
Maxwell deneylerinin belirlediği ışık hızı ether'e
göreli olarak belirleniyor olmalıydı. Gözlenen ışık hızı Galilei dönüşümü
altında olması gerektiğinden farklı ise (ki bu çok küçük bir farktır), bunun
nedeni, fizik kurallarının her eylemsiz sistemde aynı olmaması değil,
gözlemcinin eylemsizlik konuşlanmasının ether'e göre hareket ediyor olmasıydı.
Öyleyse, her şeyden önce etherin
varlığını kanıtlamak gerekiyordu. Bilimsel gelişme sürecinde, yapılması gereken
iş açık seçik ortaya çıkınca onu yapacak birileri daima ortaya çıkar. Şimdi
onun öyküsüne geçebiliriz.
Beklentilerin aksine, boşlukta ether
olmadığı, ışık hızının gözlemcinin hızına (onun bulunduğu eylemsiz sistemin
hızına) bağlı olmadığı, her sistemden aynı hızda göründüğü kanıtlandı.
Ortaya oldukça ilginç bir durum
çıkmıştı. Maxwell denklemlerine Galilei dönüşümü uygulanınca, ışık hızı bir
eylemsiz sistemden ötekine değişiyordu. Ama Michelson & Morley deneyi,
ışığın her eylemsiz sistemden aynı göründüğü sonucunu veriyor ve böylece Maxwellin
deney sonuçlarını doğruluyordu. Yani ışık, Galilei Görelilik İlkesine uymuyor,
her eylemsiz sistemde değişmez (invariant) c
değerini alıyordu.
Michelson ve
Morley
1887 yılında Michelson ve Morley adlı
iki amerikalı fizikçi, etherin varlığını kanıtlamak için ilginç bir
deney yaptılar. Deneye temel olan düşünce çok basitti. Bir ırmakta akıntıya
karşı yüzmekle akıntı yönünde yüzmek arasındaki farkı düşününüz. Sabit u hızıyla yüzen bir cisim, hızı v
olan akıntı yönünde giderse, sabit bir referans sistemine göre, hızı (u+v), akıntıya karşı giderse (u-v), akıntıya dikey yönde giderse Ö(u2+v2) olur.
Dünya, ethere göre -v hızıyla gidiyor ise, tersine olarak,
ether, dünyaya göre v hızıyla gidiyor
olacaktır. O halde, etheri v hızıyla
akan bir ırmak gibi düşünebiliriz. Dolayısıyla, etherin akış doğrultusuna
göre karşı yöne, aynı yöne ve dikey yöne
gönderilecek ışık ışınlarının hızları farklı olmalıdır.
Şekil 2.1:
Michelson-Morley Deneyi
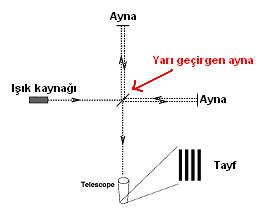 .
.
Michelson ve Morley bu basit ama
zekice düşünceden hareket ettiler. Her yöne kolay dönebilsin diye cıva içinde
yüzen bir platform kurdular ve platform üzerinde bir deney düzeneği yaptılar.
Bir ışık kaynağından çıkan ışını, birbirlerine dikey doğrultularda yerleştirilen aynalara
yönlendirdiler. Aynalardan yansıyan ışını bir interfometre ile gözlediler.
Birbirlerine dikey yönde gidip aynada yansıdıktan sonra dönen ışınların hızları
farklı olduğunda, Doppler kayması denilen olayın interferometrede görünmesi
gerekir. Platform her yöne hareket ettirilerek yapılan deneylerde, beklenen
kayma gözlenemedi. Yani ışığın hızı her yönde aynı oldu. Buradan çıkan sonuç şudur: Ya dünya
hareketsizdir, ya da ether yoktur. Dünyanın hareket ettiğine kuşkumuz
olamayacağına göre, ether yoktur sonucuna varmalıyız. Tabii, bu
deneyin verdiği asıl sonuç, ışığın her yönde aynı hıza sahip olduğudur.
Lorentz,
Poincare ve Minkowski
Şimdi problem şuna dönmüştü: Işığın
hızı neden her eylemsiz sistemde aynı görünüyordu? Bunun fiziksel yanıtıyla
ilgilenmeyen matematikçiler sorunu kolayca çözdüler. Galilei dönüşümü yerine,
ışık hızını koruyan bir dönüşüm tanımladılar. Hendrik Antoon Lorentz
(1853-1928) ışık hızını değişmez (invariant) kılan bir dönüşüm tanımladı. Henri
Poincaré, Einsteinin Özel Görelilik Kuramını yayınlamasından önce, 1904
yılında, aynı işi yapan dönüşüm gruplarını tanımladı ve sorunu matematiksel
açıdan bütünüyle çözdü. Hebert Minkowskinin kurduğu geometri, henüz ortaya
çıkmayan göreliliğin geometrik modeliydi. Böylece, görelilik kuramının
matematiksel dayanağı hazır duruma gelmişti. Ama, ışık hızını sabit gösteren
deneylere ve o hızı sabit kılan matematiksel yapılara fiziksel bir yorum
getirilmeliydi.
Bu yorumu 1905 yılında Einstein, Özel Görelilik Kuramı'nı ortaya atarak yaptı ve
böylece fizikte yepyeni ufuklar açtı. Bu ufku açıklayabilmek için Lorentz
dönüşümlerini ya da daha genel olarak Poincaré gruplarını incelemek gerekir.
Genelliği ve estetiği bakımından ikincisi tercih nedenidir. Ama kısalığı
nedeniyle, burada Lorentz dönüşümlerini ele alacağız.
Lorentz
Dönüşümü
S ve S
konuşlanma sistemlerinin başlangıç noktaları çakışsın ve S sistemi S
sistemine göre v hızıyla Ox-ekseni
boyunca hareket etsin. Başlangıç noktasını O(0,0,0,0)
ile gösterelim. S sistemindeki noktaları (t,x,y,z)
ile S sistemindeki noktaları da (t,x,y,z) ile gösterelim. Aşağıdaki denklemlerin tanımladığı
dönüşüm Lorentz dönüşümüdür:
Formül 2.2:
Lorentz dönüşümü
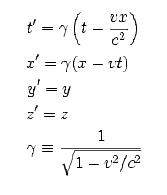
Formül 2.3: Hızların dönüşümü
Burada g Lorentz katsayısı
ve c ışığın vakum içindeki hızıdır. Şimdi S
sistemi içindeki bir gözlemci Ox-ekseni
boyunca w hızıyla hareket eden bir
cismi gözlesin. Aynı cismi, S sistemindeki gözlemci w
hızıyla gözlüyorsa, bu ikisi
arasında
![]()
bağıntısı varolacaktır. Bu bağıntıyı
yukarıdaki dönüşüm formüllerinden kolayca elde ederiz. Şimdi bu bağıntıda S sistemine göre cismin ışık hızıyla hareket
ettiğini düşünelim. w=c değerini eşitlikte yerine koyarsak w=c çıkar. Demek ki, S sistemine göre ışık
hızıyla hareket
Buradan görüldüğü gibi, bir eylemsiz
sistem ötekine göreli olarak sabit v
hızıyla gidiyorsa ve v<<c ise, Lorentz
dönüşümü Galilei dönüşümüne indirgenmiş
olur. O halde, Galilei dönüşümü, Lorentz dönüşümünün özel bir halidir.
Gerçekten, Maxwell'e kadar Galilei dönüşümüyle
bir sorun yaşanmamış olmasının nedeni, ele alınan v hızlarının
ışık hızından çok çok küçük olmasıdır.
Einstein: dahiler
başkadır !
Maxwell denklemleri ve Michelson-Morley deneylerinden
sonra Lorentz ve Poincarenin ortaya koyduğu matematiksel çözüme fiziksel bir
anlam vermek gerekiyordu. Lorentz ve Poincaré, birbirlerinden bağımsız olarak,
bir eylemsiz sistemden ötekine geçişte ışık hızını değiştirmeyen dönüşümleri
bulmuş olsalar da, buna fiziksel bir yorum getiremediler. 1905 yılında Albert Einstein (1879-1955), Özel Görelilik
Kuramını yaratan şu iki postulatı koyacaktır:
1.
Görelilik İlkesi: Mutlak dinginlik (hareketsizlik) yoktur. Bütün hareketler ya
da hareketsizlikler, gözlenen bir başka nesneye görelidir. Bir cismin dingin
halde mi, yoksa düzgün doğrusal hareket mi yaptığı mekanik deneylerle
ayırdedilemez. Başka bir deyişle, bir referans noktasına göre sabit duran bir
gözlemci ile o referans noktasına göre düzgün doğrusal hareket eden başka bir
gözlemci, bütün hareket yasalarını aynı algılarlar. Gözlemcilerin hızlarına bağlı olmaksızın fizik yasaları her eylemsiz
sistemde aynıdır.
2.
Işık hızı sabittir: Gözlemcilerin birbirlerine göre hızları ne
olursa olsun, ışık hızı bütün gözlemciler için aynıdır.
Elbette, Einstein Maxwellin deney sonucunu postülat
olarak alırken, deneyden daha sağlam
dayanaklara sahip olmalıydı. O dayanak, Lorentz dönüşümüydü. Lorentz dönüşümü
kullanılırsa, iki hızın tolamı için
Formül 2.4: Hızların toplamı

formülü geçerli olmaktadır. Şimdi, yerdeki bir
gözlemciye göre v hızıyla giden bir
arabadan ileriye doğru bir ışık ışını salınsın.
v1= c (ışık
hızı) ve v2= v (arabanın hızı) konulursa
Formül 2.5: Işık hızı her gözlemciye göre
aynıdır.
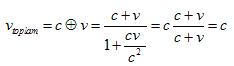
eşitliği elde edilir. Buna sayısal bir örnek verelim.
Hızları v1= 0.9c = v2 olan
iki cisim düşünelim. Newton fiziğine göre bu iki hızın toplamı 1.81c olmalıdır.
Biraz sonra açıklayacağımız gibi, hiçbir cisim ışıktan hızlı gidemeyeceğine
göre, bu olanaksızdır. Ama, Lorentz dönüşümüne göre, yukarıdaki toplam tanımını
kullanırsak
Formül 2.6: Işıktan hızlı hareket yoktur
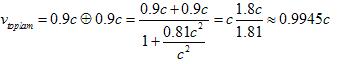
çıkar. Görüldüğü gibi, Einsteinin postülatı sağlam
bir matematiksel dayanağa sahiptir.
Bu varsayımlardan yola çıkan Einstein, Newton
Mekaniğinin temeli olan mutlak uzay ve mutlak zamanın var
olmadığını, zamanın ve uzunluğun
gözlemcinin kullandığı konuşlanma sistemine bağlı olarak değiştiğini göstermiş,
momentum ve enerji tanımlarına farklı bir bakış getirmiştir. Şimdi bunları açıklamaya çalışalım.
Einstein-Minkowski
Uzayzamanı
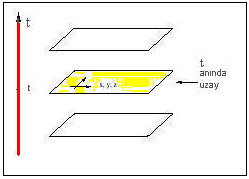
Şekil 2.7: Düz uzayzaman (flat spacetime)
Açıklamayı kolaylaştırmak için uzayı
iki boyutlu xOy-düzlemi ile, zamanı
buna dik olan Ot-ekseni ile gösterelim. Bir olayı uzaydaki bir nokta olarak
düşüneceğiz. Galilei uzay ve zaman sisteminde
zaman eksenine dik düzlemler eşanlı olayları belirler; yani xOy-düzlemine paralel bir düzlem
içindeki bütün noktalar eşanlıdır (o olaylar aynı zamanda meydana gelmiştir).
Bu mutlak zaman demektir, çünkü, bütün
gözlemciler (nerede olurlarsa olsunlar) iki olay arasındaki zaman farkını aynı
göreceklerdir.
Einstein-Minkowski uzayzamanı
yukarıdakinden farklı algılanmalıdır. Özellikle, eşanlılık ilkesi tamamiyle
farklıdır.
Işık
Konisi
Uzayzamandaki her olay (nokta) için,
aşağıdaki yöntemle bir ışık konisi kuruyoruz. Gene anlamayı görsel kılmak için
iki boyutlu uzay düşünelim. Koninin ekseni zaman eksenidir ve olaydan (tepe noktası) geçer. Koni yüzeyi,
eksenle 45 derecelik açı yapan doğrunun eksen etrafında dönmesiyle oluşur.
Böylece, tepeleri çakışık ve olaya göre simetrik iki koni ortaya çıkar. Uzay
(örneğimizde xOy-düzlemidir) Ot-zaman
eksenine diktir.
Şekil 2.8: Işık konisi
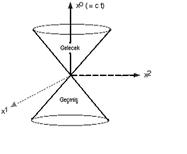
Işık konisinde birimin ışık-saniyesi
olduğunu varsayalım. Işık-saniyesi, ışığın bir saniyede aldığı yoldur. Her olay
için uzayxaman sisteminde böyle bir koni düşünebiliriz.
- Olay konilerin tepelerinin
çakışık olduğu anda olmuştur. Üstteki koni, o olayın geleceğidir. Ona gelecek ışık-konisi diyoruz.
- Alttaki koni, o olayın
geçmişidir. Ona geçmiş ışık-konisi
diyoruz.
Işık konisi şu anlamı taşır. Işık
ışınının yönü, o ışığın çıktığı kaynağın hareketine değil, ışının yayıldığı
anlık olaya bağlıdır. Ayrıca, Einsteinin Görelilik İlkesi uyarınca, bütün
gözlemciler, kendi hareketlerine bağlı olmaksızın, ışığın her yöndeki hızını
aynı ölçerler. Bu şu anlama gelir. Her olayda bütün gözlemciler ışık konisinde
anlaşırlar, onu evrensel olarak görürler.
Eşanlılık
(Eş Zamanlılık simultaneity)
Lorentz Dönüşümü'nden
sezinlenebileceği gibi, t=t' gibi basit bir bağıntı olmayacağına göre zaman göreli bir kavram halini almaktadır.
Gerçekte bunun anlamı eşanlılık
kavramının hangi eylemsiz konuşlanma sistemi içinde olduğumuza bağlı olduğudur.
Bu durum, ışık hızının hangi eylemsiz konuşlanma sistemi içinde olduğumuza
bağlı olmadığından çıkar.
Hareket halindeki bir tren vagonunun tam
ortasında bir lamba olsun. Lamba yandığında ışık hüzmesi hem trenin gidiş
yönüne hem onun ters yönüne c=3×108m/sn hızıyla yayılacaktır.
Vagonun içindeki bir gözlemci, ışığın
vagonun önüne ve arkasına aynı anda (eşanlı)
ulaştığını görecektir.
Öte yandan, tren dışındaki bir gözlemci
için durum farklıdır. Işığın hızı, gözlemcinin içinde bulunduğu eylemsiz
sisteme bağlı olmaksızın, her gözlemciye göre aynıdır ve vagonun her iki yönüne
doğru c hızıyla gider.
Vagonun arkası kendisine doğru gelen ışığa yaklaşırken, vagonun önü kendisine
doğru gelen ışıktan uzaklaşmaktadır. Dolayısıyla, ışık vagonun arkasına daha
çabuk, vagonun önüne daha geç ulaşacaktır. Demek ki, bu iki olay, yerdeki
gözlemci için eşanlı değildir.
Görüldüğü gibi, tren içindeki gözlemciye
eşanlı görünen iki olay tren dışındaki gözlemciye farklı zamanlarda olan iki
olay olarak görünmektedir.
Oyunu biraz daha eğlenceli kılmak için,
trenden daha hızlı giden bir yarış arabası içindeki gözlemcinin olayları nasıl
göreceğine bakalım.
Gene, ışığın hızının, gözlemcinin içinde
bulunduğu eylemsiz sisteme bağlı olmaksızın, her gözlemciye göre aynı olduğunu
ve vagonun her iki yönüne doğru c hızıyla gittiğini
anımsayalım. Yarış arabası trenden daha hızlı olduğu için, arabadaki gözlemciye göre tren ters yönde gitmektedir. Dolayısıyla,
vagonun önü kendisine doğru gelen ışığa yaklaşırken, vagonun arkası kendisine
doğru gelen ışıktan uzaklaşmaktadır. Dolayısıyla, ışık
vagonun arkasına daha geç, vagonun önüne daha erken ulaşacaktır. Demek
ki, bu iki olay, arabadaki gözlemci için eşanlı
değildir.
Sonuç: Bir vagonda
geçen iki olayın kronolojik sırası yerdeki, vagondaki ve trenden hızlı giden
bir araçtaki üç gözlemci tarafından farklı farklı görünmektedir. Yerdeki
gözlemciye göre önce olan olay,
arabadaki gözlemciye göre sonra olan olaydır. O halde, farklı eylemsiz sistemlerde eşanlılık olamaz.
Işıktan Daha Hızlı Hareket
Eğer öncelik,
eşanlılık ve sonralık kavramları
gözlemciye göre değişiyorsa, bir olayın başka bir olayı yarattığı nedensellik (casuality) kavramını nasıl
açıklayacağımızı ciddi olarak düşünmeliyiz.
Bunu biraz açıklamakta yarar vardır.
Eğer bir A olayı başka bir B olayının olmasının
nedeni ise, A olayı B olayından önce olmalıdır.
Ama, bir gözlemci A olayının B olayından önce
olduğunu, başka bir gözlemci ise A olayının B
olayından sonra olduğunu gözlüyorsa, nedensellik konusunda bir uyuşmazlık
ortaya çıkacaktır.
Bir A
noktasından atılan bir ok B noktasındaki elmayı vursun.
Okun atılışına A olayı, elmanın vuruluşuna da B
olayı diyelim.
Önceki bölümde ele aldığımız uzayzaman
diyagramlarını bu iki olay için tekrarlayalım:
- A da ok atıldı
- Atılan
ok A ve B yi birleştiren doğru boyunca
yol aldı.
- Ok
B ye ulaşınca elmayı vurdu.
Şekil 2.9: Eşanlılık yoktur

(x,t)
sisteminde, ok atıldıktan sonra
elma vurulur. (x',t') sisteminde, okun atılışı ile elmanın
vuruluşu eşzamanlıdır. (x'',t'') sisteminde,
elma ok atılmadan önce vurulmuş olacaktır. Bu
çelişki nereden geliyor? Biraz düşününce, çelişkinin kaynağını göreceğiz. A dan
B ye giden okun ışık hızından daha hızlı hareket ettiğini
varsayıyoruz. Oysa, görelilik kuramına göre hiç bir cisim ışık hızından
daha hızlı gidemez.
Saatlerin Eşanlaştırılması (Synchronization)
Eşanlılık kavramının
göreli oluşu bazı sonuçlar doğuracaktır. Bu sonuçlardan birisi şudur: Bir
konuşlanma sistemi içinde eşanlaştırılan (senkronize edilen) saatler başka
bir sistem içinden eşanlaşmamış (senkronize olmamış) görünür.
Zaman Gecikmesi (Time Dilation)
Eşanlılık kavramının göreliliğinin
önemli sonuçlarından birisi şudur: Farklı eylemsiz konuşlanma sistemlerinde
zamanın akış hızı farklıdır. Buna zaman
genişlemesi (time dilation) diyoruz.
İki saatin hızını karşılaştırmak için,
şöyle basit bir yol izlenebilir.
- Bir
başlangıç anı seçilir ve her iki saatin o anda (aynı anda) aynı zamanı göstermesi
(senkronize) sağlanır.
- Aradan
belli bir süre geçtikten sonraki bir anda (aynı
anda) her iki saat okunur.
Bu işi yaparken, parantez içindeki
"aynı anda" deyimini söylemeye bile
gerek görmüyoruz. Çünkü o yapacağımız mukayese için doğal
olarak gereklidir. Oysa "aynı
anda" deyimi "eşanlılık"
deyimidir. Ama biliyoruz ki, farklı gözlemcilere göre "eşanlılık" olamaz.
Formül 2.10: Zaman gecikmesi
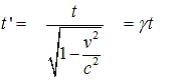
Bunu uzayzaman
çizeneğinden görebiliriz. (x,t) ve (x',t') eylemsiz
sistemlerinin başlangıç noktaları belli bir anda çakışık olsun. Bu çakışma
anında saatleri senkronize edelim. (Yukarıdaki 1. Adım). (x,t)
sistemine göre (x',t') sistemi sabit bir v
hızıyla hareket ediyor varsayalım. Bir süre sonra, saatler birbirinden
uzaklaşacak ve onları üst üste çakıştırıp aynı anda gösterdikleri zamanı okuma
olanağı kalmayacaktır. (x,t) sistemindeki
gözlemci belli bir anda kendi saati ile (x',t')
sistemindeki saati mukayese edince, öteki saatin geri kaldığını görecektir.
Tersine olarak, (x',t') sistemindeki gözlemci aynı anda kendi
saatini (x,t) sistemindeki saat ile
mukayese edince, öteki saatin geri kaldığını görecektir. Başka bir
deyişle, her gözlemci, ötekinin saatinin yavaş gittiğini görecektir. Bunun nedeni, eşanlılık
olduğunu varsaymamızdır.
Lorentz Büzülmesi
Eşansızlık kavramının sonuçlarından
birisi de uzunlukların gözlemciye bağımlı
olarak değişmesidir.
Bir şeyin uzunluğunu nasıl ölçeriz? Uzunluğu ölçülecek cismi bir eksen (skalası
olan bir doğru) üzerindeymiş gibi düşünür ve cismin iki
ucunun skaladaki karşılıklarını okur, bunlar arasındaki farkı buluruz.
Bulduğumuz fark o cismin uzunluğudur.
Acaba, konu bu kadar basit
midir? Basit olmadığını bir örnekle açıklayalım.
Bir tren vagonunun uzunluğunu
ölçmek isteyelim. Tren istasyonda duruyor iken, vagonun iki ucu arasındaki
rayın uzunluğunu ölçersek, trenin uzunluğunu bulabiliriz. Ama tren hareket
ediyorsa ne yapabiliriz? Vagonun arka ucunun ray üzerindeki izdüşümünü
işaretleyip, ön ucu için aynı işi yapmak üzere öne doğru çok çok
hızla gitsek bile, tren hareket halinde olduğu için belli bir yol alacak ve
ölçümlememiz vagonu daha uzun gösterecektir. Tersine olarak, önce vagonun
önünden ölçümlemeye başlasak, bu kez tren olduğundan daha kısa
çıkacaktır. Tabii, pratikten kaynaklanan bu sorunu çözmek kolay
görünüyor. Vagonun her iki ucun için ölçümlemeyi aynı
anda (eşanlı) yaparız. Oysa bu iş, ancak aynı konaç
sisteminde isek yapılabilir. Farklı konaç sistemlerindeki gözlemciler için eşanlılık yoktur.
Vagon içindeki gözlemci, vagonun ön ve
arkası arasındaki uzunluğu, kendi kon sistemine göre, vagonun ön ve
arka duvarlarını eşzamanlı olarak eksen üzerine izdüşürerek, vagonun
uzunluğunu L' olarak ölçsün. Yerdeki gözlemci de kendi kon sistemine
göre, vagonun uzunluğunu L olarak ölçsün. Trenin hızı v ise,
Lorentz dönüşümüne göre L ile L'
arasında
Formül 2.11 : Lorentz büzülmesi
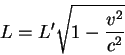
bağıntısı vardır. Buradan görüldüğü
gibi, L > L' dür. Bu demektir ki, yerdeki gözlemci
hareketli treni daha kısa görecektir. Bunun nedeni, farklı gözlemciler arasında
eşanlılık olamayışıdır. Bu etkiye Lorentz Daralması (Lorentz contraction)
diyoruz.
Hareketsiz iken cismin uzunluğuna onun
doğal uzunluğu diyoruz. Bir cismin doğal uzunluğu, hareket halindeki
uzunluğundan daha büyüktür. Başka bir deyişle, hareket eden cisimler (hareket
yönünde) daha kısa görünürler. Lorentz Dönüşümü bu daralmanın oranını
vermektedir.
Eylemsiz Kon Sistemlerinin
Denkliği
Yerdeki bir gözlemciye göre (sabit
eylemsiz kon sistemi), hareketli eylemsiz sistemdeki uzunlukların
küçüldüğünü ve saatlerin yavaşladığını
söyledik.
Öte yandan, trendeki bir gözlemciye
göre, trenin eylemsizlik kon dizgesi sabittir, yerdeki eylemsiz kon sistemi ise
(trene göre ters yönde) hareket etmektedir. Bütün eylemsiz kon sistemleri denk
olduğuna göre, trenden bakınca yerdeki uzunlukların küçüldüğünü ve
saatlerin yavaşladığını gözlemlemeliyiz.
İkizler
Çatışkısı (The Twin Paradox)
Yirminci yaş gününde ikiz kardeşlerden
birisi çok hızlı giden bir gemiyle uzay yolculuğuna çıksın. Seyahat, dünya
zamanına göre yıllar (diyelim 40 yıl)
sürsün. Dünyadaki konaç sistemine göre, hızlı uzay gemisinde zaman genişlemesi
(yavaşlaması) olacağından, seyahat eden ikiz daha az yaşlanacaktır (diyelim 10
yıl). Geri döndüğünde, dünyadaki kardeşi 60 yaşında, kendisi ise 30 yaşında
olacaktır.
Öte yandan, hareket göreli olduğu için,
uzay gemisindeki konuşlanma sistemine göre, dünya gemiden hızla (ters yönde)
uzaklaşmaktadır. Aynı nedenle, bu kez, gemideki ikiz 60 yaşında, dünyadaki ikiz
ise 30 yaşında olacaktır. Bu bir paradoks gibi görünmektedir. Çözüm için
kendinizi deneyiniz.
Kütle ve Enerji
Newton Mekaniğinde kütlesi m olan bir cisim v hızıyla hareket ediyorsa kinetik enerjisi mv2/2 dir. Oysa görelilik fiziğinde bir parçacığın
enerjisi dingin
(rest) enerji ve kinetik enerji diye ikiye ayrılır. Toplam enerji
ise bu ikisinin toplamıdır:
Enerji = Dingin Enerji + Kinetik Enerji
Öte yandan, Einsteine (1879-1955)
göre, dingin enerji dingin haldeki maddenin kütlesinden başka bir şey değildir.
Dolayısıyla, kütle ve enerji
bireşmektedir.
Covariant (Eşdeğişirlik)
Newton
Mekaniğinde ve Öklit Geometrisinde geçen invariant - değişmez terimi yerine, Einstein,
Görelilik Kuramında ve Eğri Uzayda, covariant - eşdeğişir terimini koymaktadır.
Örneğin, bir K konuşlanma sisteminden
başka bir K konuşlanma sistemine
geçildiğinde zaman, uzunluk, kütle, momentum, potansiyel, enerji fiziksel
nicelikleri Lorentz katsayısıyla orantılı değişir. Bu özelik, Özel Görelilik
Kuramının matematiksel ifadesidir. Bu kuralı basitçe ifade edebiliriz.
g Lorentz
çarpanı olmak üzere bir eylemsiz sistemden ötekine geçildiğinde zaman, uzunluk, kütle, momentum ve enerjideki
değişimler, sırasıyla, şöyledir:
t = g t, L
= g L , m = g m0 , p
= g p , E = g E .
Bunları
açık yazalım:
Formül 2.12: Eşdeğişirlik (covariance)
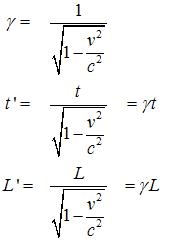
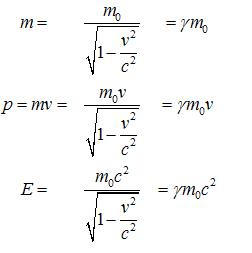
Bu
bağıntıların ışığında Özel Görelilik Kuramını daha açık ifade edebiliriz.
Özel Görelilik:
Doğa kanunları
herhangi K ve K eylemsiz
konuşlanma sistemlerinde eşdeğişimlidir. Bu demek, birisinde geçerli olan fizik
kuralı, Lorentz dönüşümü altında ötekinde de geçerlidir.
Sonuç
Esasında, Görelilik İlkesi
Galilei sisteminde mevcuttur. Konuşmanın
bu bölümünde Einsteinin Özel Görelilik Kuramının ne olduğunu açıklamaya
çalıştık. Söylenenler aklınızda karışmış olabilir. Eve götürmeniz için
aşağıdakileri ayıklıyoruz:
1.
Işığın hızı
bütün eylemsiz sistemlerde aynıdır, gözlemcinin ya da ışık kaynağının hızına
göre değişmez[1].
2.
Eşanlılık göreli
bir kavramdır. İki olayın oluş sırası, gözlemcinin eylemsiz sistemine bağlıdır.
3.
Işıktan hızlı
hareket olamaz. Olduğu taktirde, nedensellik (causality) bozulur.
4.
Zaman gecikmesi
ve uzunluk kısalması gibi ilginç fenomenler ortaya çıkar.
5.
g Lorentz
çarpanı olmak üzere bir eylemsiz sistemden ötekine geçildiğinde zaman, uzunluk, kütle, momentum ve enerjideki
değişimler Lorentz katsayısıyla orantılıdır. Bu özeliğe eşdeğişirlik
(covariant) denir.
6.
Fizik bazen eğlencelidir!
Üçüncü Bölüm
Genel Görelilik
Fizik Yasaları Evrenseldir!
Newton hareket yasaları Maxwellin elektrik ve
magnetizma denklemlerine uymuyordu. Einstein, ortaya çıkan sorunu 1905 yılında
ortaya koyduğu Özel Görelilik Kuramı
ile giderdi:
Fizik yasaları bütün eylemsiz konuşlanma sistemlerinde aynıdır.
Özel Görelilik Kuramı, fizik yasalarını (Newton hareket
yasaları, Maxwell elektromagnetizm yasaları) birbirlerine göre eylemsiz hareket
eden iki cisim için bütünüyle çözmüştür. Başka bir deyişle, Özel Görelilik
Kuramı, Newton Fiziğinin bir genellemesidir ve
bütün eylemsiz hareketleri kapsamıştır.
Eylemsiz hareket demek, düzgün doğrusal hareket
demektir. Eylemsiz hareket ivmesizdir. İvmesiz hareket eden cisim, bir referans
noktasına göre, ya bir doğru boyunca sabit bir hızla hareket eder ya da
hareketsiz durur.
Öte yandan, doğada hareketlerin çoğunluğu eylemlidir,
yani ivmeli hareketlerdir. Hızı ya da yönü değişen her hareket eylemli (ivmeli)
dir. Örneğin, üzerinde yaşadığımız dünya eylemli hareket halindedir. Özel
Görelilik Kuramı, fizik yasalarının eylemsiz konuşlanma sistemlerinde aynı
olduğunu söyler söylemez akla takılan soru şudur:
Fizik yasaları
birbirlerine göre eylemli (ivmeli) hareket eden iki cisim için geçerli değil
midir?
Bunu biraz açıklığa kavuşturmalıyız.
Fiziğin hedefi en genel doğa yasalarını
bulmaktır. Öyleyse, yalnızca eylemsiz konuşlanma sistemleriyle
yetinilemez. Doğa yasaları eylemli konuşlanma sistemleri için de geçerli
olmalıdır. Böyle olması fiziğe norm getirir, onu daha evrensel kılar. Özel
Görelilik bu yönde değerli bir başlangıçtı ve mükemmel sonuçlar sunuyordu. Ama
eylemsiz sistemlere kısıtlıydı.
Einstein, bu kısıtın kalkması gerektiğini
sezinlemişti. Ona göre, fizik yasaları her yerde her koşul altında aynı
olmalıydı. Sezgisel olarak ulaştığı bu sonucu matematik diliyle ifade etmesi
gerektiğini de biliyordu. Olağanüstü zor olan bu iş onun tam on yılını aldı.
1915 yılında, ortaya koyduğu Genel
Görelilik Kuramı fizik yasalarını önceden sezinlediği genel biçime koymuş
oldu:
Fizik yasaları
birbirlerine göre eylemli (ivmeli) hareket eden iki cisim için de geçerlidir.
Böylece, fizik yasalarının eylemli ve eylemsiz
sistemlerde aynı olduğu gerçeği kanıtlanmış oluyordu. Bu olay, fiziğe bakış
açımızı bütünüyle değiştirmiştir. Özetlersek, Özel Görelilik Kuramı, fizik
yasalarının eylemsiz konuşlanma sistemlerinde aynı olduğunu söyler. Genel
Görelilik Kuramı ise, bunu genelleştirir ve fizik yasalarının her sistemde
(eylemli ya da eylemsiz) aynı olduğunu söyler.
Basitçe ifade ettiğimiz bu büyük bilimsel bulgunun
dayandığı matematiğin anlatımı bir sömestrelik bir derstir. Bu konuşmada o uzun
dersi yapamayacağımız için, temel matematiksel dayanakları betimlemekle
yetineceğiz.
Sıradan Deneylerden
Sıradışı Düşüncelere
Einstein, damdan
düşen bir adamın kendi ağırlığını hissetmeyeceğini düşündüğü anı,
hayatının en mutlu anı olarak niteler. Çünkü o anda, Einstein, Genel Görelilik
Kuramına giden yolu görmüştür. Einsteinin düşüncelerini kavrayabilmek için
basit deneylerden başlayacağız.
Bir avucunuza ağırca bir cisim (küçük bir taş parçası,
madeni bir para vb.), öteki elinize daha hafif bir cisim (bir tahta parçası,
plastik parçası vb.) alınız. Şimdi şu basit denemeleri yapınız.
·
İki
elinizi havada dengeleyip, avuçlarınızdaki cisimlerden birinin daha ağır,
ötekinin daha hafif olduğunu hissediniz.
·
İki
avcunuzu yeterli çabuklukla yere doğru indiriniz. Avuçlarınızdaki cisimlerin
ağırlıklarının, aynı oranlarda azaldığını hissedeceksiniz.
·
İki
avcunuzu yere doğru biraz çabuk çekiniz. Avuçlarınızdaki cisimlerin
ağırlıklarının yokolduğunu, ama cisimlerin avucunuzla birlikte yere doğru
(ağırlıksız) indiğini hissedeceksiniz.
·
İki
avcunuzu yere doğru daha çabuk çekiniz. Cisimlerin avuçlarınızdan ayrılıp
havada kaldıklarını ve yere serbest düştüklerini göreceksiniz.
·
İki
avcunuzu yeterli çabuklukla yukarı doğru kaldırınız. Avuçlarınızdaki cisimlerin
ağırlıklarının arttığını hissedeceksiniz.
Bu yaptığınız deney, Genel Görelilik Kuramına temel
olan düşünceleri açıklar. Şimdi, bunları Einsteinin düşsel asansörü ile
açıklayalım.
Her yanı kapalı bir asansörde bir gözlemci ve yanında
iki taş bulunsun.
1. Asansör hiç bir kuvvetin olmadığı dış
uzayda (ağırlıksız ortam) serbest yüzüyorsa, gözlemci ve toplar hiçbir kuvvet
etkisinde kalmazlar, asansörle birlikte serbest yüzerler (Şekil 3.1).
2. Ağırlıksız ortamda, asansör bir iple
yukarı doğru çekilsin. Bir ivme oluşur, Gözlemci ve taşlar asansörün tabanına
düşerler. Asansördekiler, yukarı çekildiklerini fark edemez, gravitasyon[2]
etkisi olduğunu sanırlar (Şekil 3.2).
3.
Asansör
ağırlıksız ortamdan çıksın ve gravitasyon alanına girsin. İpe asılı kalsın ama
yukarı çekilmesin. Gözlemci ve taşlar (2) de olduğu gibi asansörün tabanına
düşerler. Gözlemci yukarı çekilmekle, gravitasyon alanında olmak arasındaki
farkı anlayamaz (Şekil 3.3).
4.
Gravitasyon
alanında asılı duran asansörün ipi kesilsin. Gözlemci ve taşlar asansörle
birlikte serbest düşmeye başlarlar. Gravitasyonsuz ortamda olduğu gibi
yüzerler. Gözlemci gravitasyonsuz ortamda olmakla, gravitasyon alanında serbest
düşme arasındaki farkı anlayamaz (Şekil 3.4).
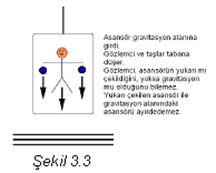
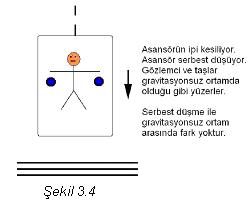
5.
Asansör
yerküre gravitasyon alanında asılı dururken gözlemci ve taşlar yerküre
merkezine doğru çekilir. Gözlemci yere doğru düşen taşların birbirlerine
yaklaştığını fark eder (Şekil 3.5).
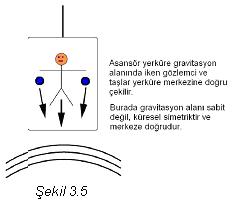
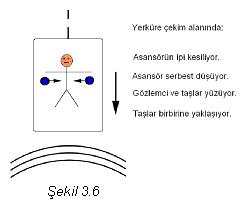
6.
Yerküre
gravitasyon alanında asılı duran asansörün ipi kesiliyor. Asansör serbest
düşüyor. Gözlemci ve taşlar asansörde yüzmeye başlıyor. Gözlemci, taşların
birbirlerine yaklaştığını görecektir (Şekil 3.6).
Yukarıda anlatılan düşsel asansör deneylerinden
çıkarılacak sonuçlar şunlardır:
i)
İvmeli
hareketle gravitasyon etkisiyle hareket arasındaki fark, yerel olarak, ayırt
edilemez (1. ve 2. deney).
ii)
Gravitasyonun
etkisi serbest düşmeyle, yerel olarak, yokedilebilir (3. ve 4. deney).
iii)
Düzgün
olmayan bir gravitasyon alanında, yerel olarak, serbest düşmeye geçilerek
gravitasyonun etkisi yokedilemez (5. ve
6. deney).
Newtonun mutlak uzay varsayımı eylemsizlik ivmesine
(direncine) ve merkezkaç kuvvetlere dayanır. Newton Mekaniğinin, bir cismin mg gravitasyon ivmesi ile mi eylemsizlik ivmesini
kuramsal açıdan farklı gördüğünü, ama Eötvösün 108 de bir duyarlılıkla
yaptığı deneylerde ikisi arasında pratik açıdan bir fark görülemediğini
söylemiştik. Buna ek olarak, Galilei yasası uyarınca ağır ve hafif cisimler
aynı hızla yere düşerler. Newtonun gök cisimleri arasındaki F=mMG/r2 çekim kuvvetinden,
çekim ivmesinin cismin m kütlesine
bağlı olmadığını söylemiştik. Bütün bunlar bir arada düşünülünce, bu yasaların
hepsini içine alan daha genel bir fizik yasasının varolduğunu düşünmek doğal
olmaktadır. Einstein da böyle düşündü ve
Yerel olarak : Gravitasyon = Eylemsizlik = İvme
olduğunu gördü. Bu eşitlik çok şaşırtıcı değildir.
İvmeyi ikinci basamaktan türev belirliyor. Eylemsizlik cismin düzgün
hareketinin (dingin de olabilir) değişmesini engellemeye çalışan kuvvettir.
Düzgün hareketin değişmesi demek, cismin ivme kazanması demektir. O halde,
eylemsizlik kuvveti ivmeye karşı koyan bir kuvvettir. Etki-tepki yasası
uyarınca eylemsizlik = ivme eşitliği
doğal bir sonuçtur. Öte yandan, gravitasyonun etkisinin serbest düşmeyle
(eylemsizlik), yerel olarak, yokedilebileceğini söylemiştik.
Eğri Uzay
Öklit Geometrisinde iki nokta arasındaki en kısa
yolun doğru[3]
olduğunu öğretirler. Burada en kısa yol deyimi uzaklık kavramıyla ilgilidir. Öklit
geometrisinde uzaklık bir metrik (fonksiyon) ile tanımlanır. P(x1,y1,z1)
ile Q(x2,y2,z2) noktaları arasındaki uzaklık (metrik)
![]()
bağıntısıyla verilir.
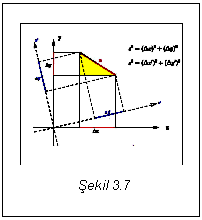 Bilindiği gibi bu metrik katı dönüşümler altında
değişmez. Katı dönüşüm deyiminden
öteleme (paralel kayma) ve dönme dönüşümlerini anlıyoruz. Katı dönüşümler uzunluğu
ve açıyı değiştirmez. Öklit geometrisinde geçerli olan bu kurallar başka
geometrilerde başka biçimlere girebilir. Örneğin, Lizbondan Newyorka gidecek
gemi ya da uçak, en kısa yoldan gitmek isterse, iki kentten geçen paralel
daireyi izlemez. Kaptanlar bu iki kentten geçen büyük çember üzerinde giderler.
Bu nedenle, yolcular önce kuzeye doğru çıkıldığı sonra güneye doğru inildiği
izlenimini edinirler. Çünkü, küre üzerindeki P noktasından bir Q noktasına giden en kısa yol P
ve Q dan geçen büyük çember yayıdır[4].
Öklit uzayındaki
Bilindiği gibi bu metrik katı dönüşümler altında
değişmez. Katı dönüşüm deyiminden
öteleme (paralel kayma) ve dönme dönüşümlerini anlıyoruz. Katı dönüşümler uzunluğu
ve açıyı değiştirmez. Öklit geometrisinde geçerli olan bu kurallar başka
geometrilerde başka biçimlere girebilir. Örneğin, Lizbondan Newyorka gidecek
gemi ya da uçak, en kısa yoldan gitmek isterse, iki kentten geçen paralel
daireyi izlemez. Kaptanlar bu iki kentten geçen büyük çember üzerinde giderler.
Bu nedenle, yolcular önce kuzeye doğru çıkıldığı sonra güneye doğru inildiği
izlenimini edinirler. Çünkü, küre üzerindeki P noktasından bir Q noktasına giden en kısa yol P
ve Q dan geçen büyük çember yayıdır[4].
Öklit uzayındaki ![]() doğrusunun yerini
kürede
doğrusunun yerini
kürede ![]() büyük çember yayı
almıştır (Şekil 3.8). Başka yüzeylerde başka biçimler alacaktır. Örneğin,
silindir yüzeyinde başka, hiperboloid yüzeyinde başkadır. (Görelilikte
kullanılan terimlere uyum sağlamak için, Öklit uzayına düz uzay flat space- , Öklit dışı
uzaylara da eğri
uzay curved space- diyeceğiz.)
büyük çember yayı
almıştır (Şekil 3.8). Başka yüzeylerde başka biçimler alacaktır. Örneğin,
silindir yüzeyinde başka, hiperboloid yüzeyinde başkadır. (Görelilikte
kullanılan terimlere uyum sağlamak için, Öklit uzayına düz uzay flat space- , Öklit dışı
uzaylara da eğri
uzay curved space- diyeceğiz.)

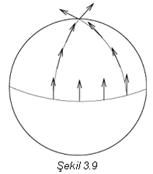

Öklit uzayında bir vektörü, kendisine paralel olarak,
kapalı bir eğri boyunca kaydırarak (öteleme) ilk noktaya kadar getiriniz.
Vektörün orijinal vektörle çakıştığını göreceksiniz. Ama küre üzerinde bu
özelik bozulur. Başka bir deyişle, küre üzerinde paralel kayma yola bağlı
olarak değişir (Şekil 3.9). Bu özelikten yararlanarak, yüzeyin eğriliğini
(curvature) hesaplarız (Şekil 3.10). Diferensiyel Geometri derslerinde,
eğriliğin ikinci basamaktan türevle hesaplandığını anımsayınız. Öte yandan,
fizik derslerinde, ivmenin de ikinci basamaktan türevle hesaplandığını
gördünüz. Buradan, ivme ile eğrilik arasında bir ilişki kurulabileceği
sezilmektedir. Öte yandan, gravitasyonun ivmeye eşit olduğunu söyledik. O
halde, gravitasyon ile eğrilik arasında bir ilişki doğmaktadır. Bütün bu
söylediklerimizin matematiksel kanıtı vardır. Kanıtlarına giremeyeceğimiz Genel
Görelilik Kuramının matematiği bunu yapmaktadır.
Uzayzamanda her olayı bir nokta ile göstereceğiz. İşin
içine zaman girdiği için, uzayzamanda iki nokta arasında Öklit
geometrisindekine benzer bir uzaklıktan sözedemeyiz. Noktalar arasındaki uzaklık
terimi yerine, iki olay arasındaki uzayzaman aralığı terimini kullanacağız. Buna
göre, Dt süresi
içinde uzay koordinatlarındaki değişim Dx , Dy , Dz ise, uzayzaman
aralığı aşağıdaki bağıntı ile tanımlanır:
![]()
Bu bağıntı Minkowski metriği diye bilinir. Öklit
metriği negatif değer alamazdı. Ama Minkowski metriği negatif ve pozitif
değerler alabileceği gibi, farklı olaylar (noktalar) için sıfır değerini bile
alabilir. Burada c bir dönüşüm sabitidir ve pratikte onu ışık hızı olarak kabul edeceğiz. Bu metrikte önemli olan şey,
fotonların c hızıyla gitmesinden çok, koordinat dönüşümleri altında
uzayzaman aralığını değişmez kılan bir c sabitinin varlığıdır. Başka bir
deyişle, (t,x,y,z) eylemsiz
sisteminden (t,x,y,z) eylemsiz
sistemine geçilirse aşağıdaki eşitliği sağlayan bir c sabiti vardır.
![]()
Matematikçiler Minkowski metriğini daha zarif yollarla
tanımlamayı ve Görelilik Kuramını sağlam bir matematiksel yapı içine almayı
severler. Bu yönde yapılanlar öğrenilmeye değecek zerafet ve çekiciliktedir.
Halen aktif çalışma alanı olan Gauge
Kuramı, String Kuramı gibi kuramlar, Einsteinin kullandığı tensör yerine
başka matematiksel yapılar koymaktadır. Bunların her birisi bu konuşmaya
sığmayacak büyüklüktedir. O nedenle, işin matematiğini yapmak yerine,
Einsteinin yaptıklarını betimlemekle yetinmek zorundayız.
Tensör hesapta bir noktanın koordinatları alt
indislerle değil üst indislerle gösterilir. İşlemlerde, bileşen sayıları
onlarla sayılacak kadar çok olduğu için kısaltmalar kullanılır. Örneğin,
uzayzamanda dört boyutlu bir noktayı (olayı) göstermek için grek üs kullanılır.
Zaman boyutunu dışlayıp uzaydaki üç boyutu belirtmek istersek, grek üs değil,
latin üs kullanacağız:
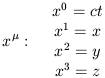
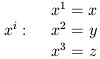
Uzayzaman aralığını daha kısa yazabilmek için, adına
metrik denen

matrisini kullanacağız. Einstein basitliği seven bir
insandı. Çok sayıda indisli terimlerin toplamını yazmak için kolay bir kısaltma
önerdi. Aynı üs ya da indis taşıyan terimler bütün mümkün haller için toplanır.
Buna göre, yukarıdaki uzunluk formülünü şu zarif biçimde yazabiliriz :
![]()
Uzayzamanda koordinat sistemlerimiz çok sık
değişecektir. Koordinat sistemi değişince, yukarıda tanımlanan Minkowski
metriğinin değişmez (invariant) kalmasını isteriz. O halde, uzayzamanda hangi
dönüşümlerin metriği (uzunluğu) değiştirmediğini bilmeliyiz. Bunu matris yardımıyla söylersek,
![]() ya da daha kısa olarak
ya da daha kısa olarak ![]()
bağıntısını sağlayan
L matrislerini (dönüşümler) bilmeliyiz. Kolayca
görüleceği gibi,
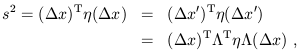
çıkar ve buradan
![]() buluruz. Bu da
buluruz. Bu da
![]() olması demektir. Bu eşitliği sağlayan
matrislere Lorentz dönüşümleri denir. Lorentz dönüşümleri çarpma işlemine göre
bir grup oluşturur. Poincaré, Lorentz dönüşümlerine ötelemeleri de ekleyerek
daha genel dönüşüm grubunu oluşturmuştur. Her iki grup da komutatif değildir.
olması demektir. Bu eşitliği sağlayan
matrislere Lorentz dönüşümleri denir. Lorentz dönüşümleri çarpma işlemine göre
bir grup oluşturur. Poincaré, Lorentz dönüşümlerine ötelemeleri de ekleyerek
daha genel dönüşüm grubunu oluşturmuştur. Her iki grup da komutatif değildir.
Minkowski Geometrisinin yapısını açıklayabilmek için
tensör kavramına girmek gerekir ki biz ona giremeyeceğiz. Ama Genel Görelilik
için matematiksel yapının nasıl kurulduğunu betimleyebiliriz.
Newton Mekaniği mutlak uzay ve mutlak zamanı
varsaydığı için, kartezyen koordinat sistemi matematikte olduğu gibi Newton
Mekaniğinde mükemmel bir araç olmaktadır. Fiziksel fenomenlerin çoğunu türev ve
integral yardımıyla açıklarız. Uzayzamana bunu taşıyabilsek sorunlar çözülmüş
olacaktı. Ama uzayzamanda bunu doğrudan yapamıyoruz.
Einstein, bu engeli aşabilmek için harika bir yol
buldu. Düşüncesi, matematik analizde yaptığımız basit bir kavrama dayanıyordu.
İvmeli hareket eden bir parçacığı düşünelim. Zaman dilimlerini durmadan
küçültelim. Her adımda, zaman dilimlerinin uç noktaları arasındaki hız farkı
giderek küçülecektir. Zaman dilimlerinin uzunluğunu sıfıra yaklaştıran sürecin
(limit konumu) sonunda anlık hız ortaya çıkacaktır. Anlık hız sabittir, yani
cisim ivmesizdir. Tam bu anda iken cismi bir eylemsiz konuşlanma sistemi içine
koyabiliriz. Bunu yaptığımız anda Özel Görelilik Kuramının bütün sonuçlarını o
an için uygulayabiliriz. Bu düşünceyle Einstein şu ilkeyi koydu
Einstein: Eşdeğerlik İlkesi
l Keyfi bir gravitasyon alanındaki uzayzamanın her noktası için öyle yerel
eylemsiz (serbest düşen) bir konuşlanma sistemi seçilebilir ki, noktanın
yeterince küçük komşuluğunda doğa yasaları ivmesiz kartezyen koordinat
sistemindeki biçimi (form) alır.
Tabii, burada ortaya şu sorun çıkıyor.
İvmeli cisim için her an farklı bir hız vardır.
Öyleyse, her an için farklı bir eylemsiz konuşlanma sistemi olacaktır. O
halde, bir sistemden ötekine dönüşümü kolayca yapacak bir yöntem gerekir.
Açıktır ki bu bir matematiksel yapı içinde gerçekleşebilir. Einstein bu iş için
tensörleri kullandı.
Matematikte hep yaptığımız gibi,
konuyu önce eldeki nesnelerden arındırıp, yapıyı soyutlaştırmak işimizi
kolaylaştıracaktır. Bir M kümesi düşünelim. Bu küme üzerine bir topolojik yapı
koyalım. Sonra yerel olarak Rn
Öklit uzayına benzetelim. Böylece M bir çokkatmanlı (manifold) olur.
Sonra bir bağlantı (connection) kuralım, üzerinde bir metrik tanımlayalım.
Böylece bir Riemann manifoldu elde edilir. Bu manifoldun her noktasına Öklit
koordinat sistemleri iliştirilebilir ve bunlar arasında düzgün dönüşümler
yapılabilir.
Şekil 3.11

Bundan sonrası uzun ve ciddi
matematiksel işlemler gerektirir. Sonuçta Genel Görelilik Kuramı gravitasyonu
uzayzamanın eğriliği olarak açıklar. Einstein alan denklemleri (field
equations) tensörel biçimiyle çok yalın görünür. [Zaten Einstein bütün
bulgularını böyle yalın biçimlerde vermiştir.]
![]()
Genel Göreliliğin tensör hesaba dayanan işlemlerinde
sağdaki ve soldaki indislerin her birisinin dörder değeri olduğunu,
dolayısıyla, yukarıda alan denklemleri dediğimiz eşitliğin 4x4x4x4=256 denklem içerdiğini söylemek gerekir. Ancak, simetriler
nedeniyle denklem sayısı 10a düşer. Einstein bu denklemlerin uzun süre çözülemeyeceğini
sanıyordu. Ama, Schwarzchild bir yıl geçmeden bir çözüm buldu. Halen, farklı
parametrelerle çözüm arayan araştırmacılara raslayabilirsiniz.
Özel ve genel görelilik
Kuramları Arasındaki Önemli Farklar:
1.
Özel
Görelilik Kuramında mutlak hızdan sözedemeyiz. Ancak, eylemsiz
sistemlere göreli
hızdan sözedebiliriz. Bunun nedeni, hızların 4-boyutlu uzayzamanda
birer vektör olarak temsil edilmesidir. Bir eylemsiz sistemden ötekine
geçildiğinde hız vektörünün yönü değişecektir.
Özel Görelilik Kuramında ise, uzayzamanın aynı
noktasında olmayan cisimlerin göreli hızlarından bile sözedemeyiz. İki cismin,
uzayzamanın aynı noktasında olmaları demek, aynı yerde aynı zamanda (eşanlı)
olmaları demektir. Farklı noktalardaki cisimlerin hızlarını karşılaştırmak
istediğimizde, önümüze olanaksız bir durum çıkar. Çünkü, bir vektörü başka bir
vektörle karşılaştırmak için birisini kendisine paralel kaydırarak (öteleme)
ötekinin üstüne çakışıp çakışmadığına bakmak gerekir. Oysa eğri uzayda paralel
kayma yola bağlıdır. Dolayısıyla, farklı noktalardaki iki cismin hızları
karşılaştırılamaz.
2.
Özel
Görelilik Kuramında bir eylemsiz koordinat sistemini, her biri ötekine göre
dingin (hareketsiz) duran saatlerin (vektör) alanı gibi düşünebiliriz.
Genel Görelilik Kuramında böyle bir
düşünceye yer yoktur. Ancak aynı noktada olan saatlerin göreli hızlarını
karşılaştırabiliriz. Başka bir deyişle, fizikte çok önemli rolü olan eylemsiz
sistemler genel görelilikte yoktur.
3.
Fizik
yasalarını eylemsiz sistemlerdeki nitelikleriyle Genel Görelilikte de kullanmak
istiyoruz. O nedenle, yerel olarak eylemsiz sistemleri uzayzamana
yerleştiriyoruz. Burada yerel terimi önemlidir. Bu işi ancak uzayzaman
aralığının sıfıra gittiği limit halde yapabiliriz. Başka bir deyişle, iki
cismin anlık hızlarını karşılaştırabiliriz.
4.
Bir
parçacık gravitasyondan başka bir etki altında değilse, ona serbest düşüyor
denilir. Bir test parçacığı deyince
enerjisi ve momentumu çok küçük olduğu için uzayzaman eğriliğine etki etmeyen
bir cismi anlayacağız. Genel görelilikte, serbest düşen bir test parçacığının
yörüngesi bir jeodeziktir. Bunun hız vektörü ise jeodezi boyunca paralel kayan
teğet vektördür.
5.
Genel
Görelilik Kuramında gravitasyon geröek bir kuvvet değildir. O uzayzamanın
eğriliğinin ortaya koyduğu bir fenomendir. [Dikkat: uzayın eğriliği değil,
uzayzamanın eğriliği].
KAYNAKLAR
Özel ve Genel Görelilik Kuramını anlatan çok sayıda kaynak
vardır. Bu büyük çeşitlilik içinde çok iyi kitaplar yanında, çok kötü yazılmış
olanlar da vardır. Bu arada çok kötü çeviriler de görebilirsiniz. İnternette
sayısız kaynağa erişilebilmektedir. Bunların da bazıları özenle hazırlanmış
yararlı kaynaklardır. Ortaya konuluşundan bu yana yüz yılı aşan bu kuramı
anlatmak için söylenmemiş söz, verilmemiş örnek, çizilmemiş diyagram kaldığını
sanmıyorum. Örnekler ve diyagramlar artık anonimdir. Thales teoremine kaynak
göstermek ne anlam taşırsa, bu yazıya kaynak göstermek de o anlamı
taşıyacaktır. Kaynak yerine, bu metnin orijinal olmadığını, anonimden
derlemeler olduğunu söylemek daha doğru olacaktır.